机器学习题解（二）—— 神经网络

ex3.m

Part 1: Loading and Visualizing Data

• Load Training Data

load('ex3data1.mat'); % training data stored in arrays X, y

• Visualization

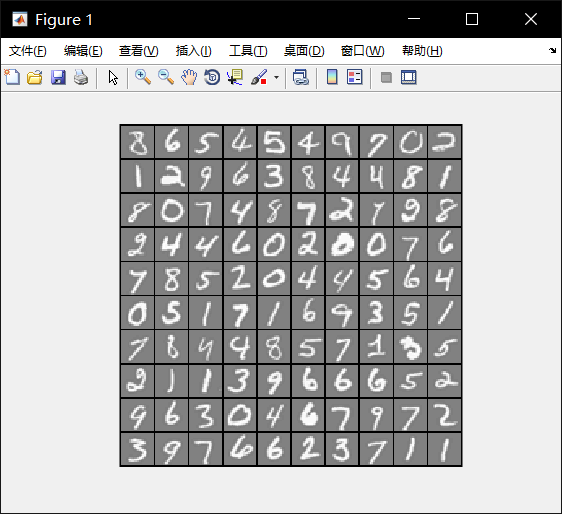
Part 2a: Vectorize Logistic Regression

• Compute the cost of a particular choice of theta. You should set J to the cost.
  Compute the partial derivatives and set grad to the partial derivatives of the cost w.r.t. each parameter in theta

J = (1 / m) * sum(-y .* log(sigmoid(X * theta)) - (1 - y) .* log(1 - sigmoid(X * theta))) + (lambda / (2 * m)) * sum(theta(2:size(theta)) .^2);

temp = theta;
temp(1) = 0;
grad = (1 / m) * (X' * (sigmoid(X * theta) - y)) + (lambda / m) * temp;

Part 2b: One-vs-All Training

• You should complete the following code to train num_labels logistic regression classifiers with regularization parameter lambda.

% Set Initial theta
initial_theta = zeros(n + 1, 1);
% Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 50);
for c = 1: num_labels
      all_theta(c, :) = fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), initial_theta, options);

Part 3: Predict for One-Vs-All

• Complete the following code to make predictions using your learned logistic regression parameters (one-vs-all).

predict = sigmoid(X * all_theta');
[~,p] = max(predict, [], 2); % ~ means ignore this 1st parameter output

ex3_nn.m

• Complete the following code to make predictions using your learned neural network.

X = [ones(m, 1) X];
z1 = sigmoid(X * Theta1');
z1 = [ones(m, 1) z1];
z2 = sigmoid(z1 * Theta2');

[~, p] = max(z2, [], 2);

ex4.m

Part 3: Compute Cost (Feedforward)

• Feedforward the neural network and return the cost in the variable J. After implementing Part 1, you can verify that your cost function computation is correct by verifying the cost computed in ex4.m

% input layer
a1 = X;

% hidden layer
X = [ones(m, 1) X];  % 5000 * (1 + 400) = 5000 * 401
z2 = Theta1 * X'; % (25 * 401) * (401 * 5000) = 25 * 5000
a2 = sigmoid(z2); % 25 * 5000

% output layer
a2 = [ones(m, 1) a2']; % 5000 * (1 + 25) = 5000 * 26
z3 = Theta2 * a2'; % (10 * 26) * (26 * 5000) = 10 * 5000

% recode the labels as vectors containing only values 0 or 1
y_vec = zeros(num_labels, m); % 10 * 5000
% put value 1 for every iterated column
for i = 1: m
    y_vec(y(i), i) = 1;
end;

% cost function
h_theta = sigmoid(z3);
J = (-1 / m) * sum(sum(y_vec .* log(h_theta) + (1 - y_vec) .* log(1 - sigmoid(h_theta))));

Part 4: Implement Regularization

• You should now add regularization to your cost function. Notice that you can first compute the unregularized cost function J using your existing nnCostFunction.m and then later add the cost for the regularization terms.

% regularized cost function
theta1 = Theta1(:, 2:size(Theta1, 2)); % size(Theta1, 2) returns the nums of locumns in the matrix
theta2 = Theta2(:, 2:size(Theta2, 2));

J = J + lambda / (2 * m) * ( sum(sum(theta1 .^ 2)) + sum(sum(theta2 .^ 2)) ); % !sum up separately

Part 5: Sigmoid Gradient

• Implement the sigmoid gradient function

g = sigmoid(z) .* (1 - sigmoid(z));

Part 6: Initializing Pameters

• Initialize W randomly so that we break the symmetry while training the neural network

% Randomly initialize the weights to small values
epsilon_init = 0.12;
W = rand(L_out, 1 + L_in) * 2 * epsilon_init - epsilon_init;

Part 7: Implement Backpropagation

• Implement the backpropagation algorithm to compute the gradients Theta1_grad and Theta2_grad.

for t = 1:m
    % Step1
    a1 = X(t, :); % 1 * 401
    a1 = a1'; % 401 * 1
    z2 = Theta1 * a1; % (25 * 401) * (401 * 1) = 25 * 1
    a2 = sigmoid(z2); % 25 * 1
    
    a2 = [1; a2]; % add bais, (25 + 1) * 1 = 26 * 1
    z3 = Theta2 * a2; % (10 * 26) * (26 * 1) = 10 * 1
    a3 = sigmoid(z3); % 10 * 1
    
    % Step2
    delta_3 = a3 - y_vec(:, t); % 10 * 1

    % Step3
    delta_2 = (Theta2' * delta_3) .* sigmoidGradient([1; z2]); % add bais, 26 * 1
    
    % Step4
    delta_2 = delta_2(2: end); % 25 * 1
    
    Theta1_grad = Theta1_grad + delta_2 * a1'; % 10 * 25, !sum up grad
    Theta2_grad = Theta2_grad + delta_3 * a2'; % 10 * 25
end
    %Step5
    Theta1_grad = (1 / m) * Theta1_grad;
    Theta2_grad = (1 / m) * Theta2_grad;

Gradient checking

% take a look and try to understand
numgrad = zeros(size(theta));
perturb = zeros(size(theta));
e = 1e-4;
for p = 1:numel(theta)
    % Set perturbation vector
    perturb(p) = e;
    loss1 = J(theta - perturb);
    loss2 = J(theta + perturb);
    % Compute Numerical Gradient
    numgrad(p) = (loss2 - loss1) / (2*e);
    perturb(p) = 0;
end

Part 8: Implement Regularization

• Implement regularization with the cost function and gradients.

Theta1_grad(:, 2:end) = Theta1_grad(:, 2:end) + (lambda / m) * Theta1(:, 2:end);
Theta2_grad(:, 2:end) = Theta2_grad(:, 2:end) + (lambda / m) * Theta2(:, 2:end);