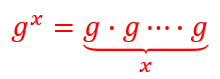Hyper の 个人博客

交流技术，分享生活

0%

公钥密码算法可证明安全理论：第二讲

发表于 更新于 分类于 ， ， 阅读次数：
本文字数： 6.2k 阅读时长 ≈ 6 分钟

3 基于群的密码学基础

3.1 有限域 Finite Field

3.1.1 有限域的定义

def 有限域（伽罗瓦域）用 (F,+,∗)(F, +, ∗) 表示，是一个包含有限数量元素的集合，其两个二进制运算加法 ++ 和乘法 ∗∗ 定义如下：

  • ① 封闭性：对∀u,v∈F∀u, v ∈ F，有 u+v∈Fu + v ∈ F 且 u∗v∈Fu ∗ v ∈ F

  • ② （加法）结合律：对 ∀u1,u2,u3∈F∀u_1, u_2, u_3 ∈ F，有 (u1+u2)+u3=u1+(u2+u3)(u_1 + u_2) + u_3 = u_1 + (u_2 + u_3) 且 (u1∗u2)∗u3=u1∗(u2∗u3)(u_1 ∗ u_2) ∗ u_3 = u_1 ∗ (u_2 ∗ u_3)

  • ③ 交换律：对 ∀u,v∈F∀u, v ∈ F，有 u+v=v+uu + v = v + u 且 u∗v=v∗uu ∗ v = v ∗ u

  • ④ 单位元：对 ∃0F,1F∈F∃0_F, 1_F ∈ F 和 ∀u∈F∀u ∈ F，有 u+0F=uu + 0_F = u 且 u∗1F=uu ∗ 1_F = u

  • ⑤ 负元：对 ∀u∈F∀u ∈ F，∃–u∈F∃–u ∈ F 使得 u+(–u)=0Fu + (–u) = 0_F

  • ⑥ 去零元：对 ∀u∈F∗∀u ∈ F^∗, ∃u−1∈F∗∃u^{−1} ∈ F^∗ 使得 u∗u−1=1Fu ∗ u^{−1} = 1_F，其中 F∗=F/0FF^∗ = F/{0_F}

  • ⑦ 分配律：对 ∀u1,u2,v∈F∀u_1, u_2, v ∈ F，有 (u1+u2)∗v=u1∗v+u2∗v(u_1 + u_2) ∗ v = u_1 ∗ v + u_2 ∗ v

3.1.2 域运算

可扩展至减法和除法：

  • 减法：由⑤有 u−v=u+(−v)u − v = u + (−v)，其中 −v-v 是 vv 的加法逆元

  • 除法：由⑥有 u/v=u∗v−1u/v = u ∗ v^{−1}，其中 v−1v^{−1} 的乘法逆元

3.1.3 域的选取

一般选取一组大素数以防止爆破攻击，因此 p(x)=p0+p1x+p2x2+⋯+pn−1xn−1∈Fp(x)p(x)=p_0+p_1 x+p_2 x^2+⋯+p_{n-1} x^{n-1}∈F_p (x) 是不可约（irreducible）的，其系数仍在 FpF_p 级别。可约的情况譬如：x2−2x^2 - 2

  • 基础域：用 (Fp,+,∗)(F_p, +, ∗) 表示

  • 扩域（extended field）：用 (Fpn,+,∗)(F_{p^n}, +, ∗) 表示

3.2 循环群 Cyclic Groups

3.2.1 群的定义

  • 阿贝尔群：用 (H,⋅)(H, ·) 表示，是一组具有二元运算 ⋅· 的元素，满足①~⑤

  • 循环的阿贝尔群：在满足①~⑤的前提下，群内任意元素均可由生成元 hh （群的方幂）生成，即：H=h0,h1,h2,⋯,h∣H∣−1H={h^0,h^1,h^2, ⋯,h^{|H|-1}}，其中群 HH 的阶 ∣H∣|H| 满足 h∣H∣=h0=1Hh^{|H|}=h^0=1_H

  • 素数阶的循环阿贝尔群：如果群 GG 是循环群 HH 的子群且 ∣G∣|G| 为素数，则 GG 是素数阶的循环子群，其中是 ∣G∣|G| 是 ∣H∣|H| 的除数，存在生成元 g∈Hg ∈ H 生成群 GG

3.2.2 素数阶的循环群

1. 使用循环群和素数阶的原因？

  • GG 是没有禁闭攻击（confinement attack）的最小子群。禁闭攻击是指攻击者试图将计算限制在一个特定的子群中，从而破坏整个方案的安全性；同时，若 GG 包含了不必要元素，可能带来不必要的复杂性和开销

    • 目前，p=2160p=2^{160} 的 160bit 长度以上比较安全，因破解离散对数问题需要 O(p1/2)O(p^{1/2})，达 80bit 安全

  • 除 g0g^0 之外的任何元素都是 GG 的生成元

  • {1,2,⋅⋅⋅,p−1}\{1, 2, · · · , p-1\} 中的任意整数都具有模乘逆元

  • 对任意 x∈Zp∗={1,2,⋯,p−1}x∈Z_p^∗=\{1,2,⋯,p-1\}，均能计算 g1/x=gx−1g^{1/x}=g^{x^{-1}}

2. 若要为密码学方案构造一个群，需要指定哪些参数？

(G,g,p)(G, g, p)：

  • GG：群的空间，是一个包含元素的集合，这些元素作为群成员

  • gg：群的生成元

  • pp：群的阶

3. 每个组元素的表示大小是多少？

对素数 pp，有 G={g0,g1,⋅⋅⋅,gp−1}G = \{g^0,g^1, · · · ,g^{p-1}\}

  • 群中有 pp 个元素，每个元素具有相同的大小

  • 群中的每个元素都可以编码为二进制字符串

  • 群中的每个元素必须用不同的二进制字符串表示

3.2.3 群幂 Group Exponentiations

设 (G,g,p)(G, g, p) 为循环群，x∈Zpx∈Z_p，用 gxg^x 表示群幂：

  • 群幂由上述定义中的群运算的 x−1x−1 个副本（copies）组成

  • 当 xx 大于 21602^{160} 时，执行 x−1x−1 个副本的计算是不切实际的

  • 存在快速计算群幂的算法：平方乘法（square-and-multiply）算法

3.2.4 离散对数问题 Discrete Logarithms Problem

群中最基本的难题是离散对数问题，给定 g,h∈G/1Gg, h∈G/{1_G}，有：

  • 满足 gx=hg^x= h 的整数 xx 称为离散对数

  • 计算 xx 称为离散对数问题

1. 群使用素数阶的另一原因？

如果 GG 是素数阶的群，则对于任意两个群元素 g,h∈G/1Gg, h∈G/{1_G}，离散对数 xx 必须存在

2. 破解离散对数问题的时间复杂度？

设 (G,g,p)(G, g, p) 为任意群，求解 DLP 的最有效算法需要 O(p1/2)O(p^{1/2})

3. 若要为密码学方案构造一个群，需要考虑哪些攻击？

  • 泛型攻击（generic attacks）：参数必须满足 p≥2160p ≥ 2^{160}

  • 特定攻击（specific attacks）：为特定群构造的所有其他参数必须足够大，譬如群元素大小

3.2.5 来自有限域的循环群

有限域 (Fpn,+,∗)(F_{p^n},+,∗) 已包含的两类群：(Fpn,+)(F_{p^n},+) 和 (Fpn∗,∗)(F_{p^n}^∗,∗)；此外引入椭圆曲线 ECC 上的群

1. 为什么要使用椭圆曲线上的群？

  • 同等安全性下，ECC 短于基于域的元素长度，存储开销低适用受限设备

    • 原因：只需要存储 x 坐标 + 0/1（上方 / 下方）的一个比特

3.2.6 群的选取

  • 乘法群 (G,g,p,q)(G, g,p,q)

    • 群的元素：从 Zp∗={1,2,⋯,p−1},∣g∣=log2pZ_p^∗=\{1,2,⋯,p-1\}, |g| =log_2 p 中选取的整数
    • 群的生成元：gg 从 Zp∗Z_p^∗ 中选取，注意不是 Zp∗Z_p^∗ 中所有的整数都是生成元
    • 群的阶：q∣(p−1)q|(p − 1)，qq 和 p−1p-1 同余
    • 群的运算：u⋅v=u×vmodpu · v = u × v mod p
    • 安全性：为达到 80bit 安全，qq 应至少为 1024 bits

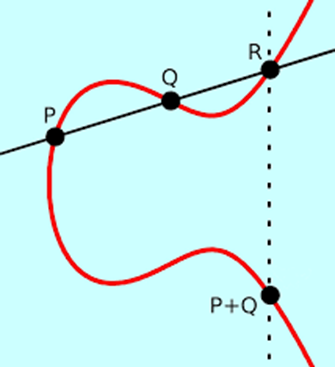
  • 椭圆曲线上的群 (G,g,p)(G, g, p)：椭圆曲线是一条定义在 FpnF_{p^n} 上的光滑曲线，所有的点都在 y2=x3+ax+by^2=x^3+ax+b 上，其中 a,b∈Fpna,b∈F_{p^n}

    • 群的元素：椭圆曲线上的点集，每个点用 x 坐标和 y 坐标表示
    • 群的生成元：gg 亦为一个点
    • 群的阶： pp 是素数阶
    • 群的运算：对 u,v∈Gu,v∈G 和 x∈Fpx∈F_p，计算 u+vu+v 或 x⋅ux·u
    • 安全性：群元素大小可以与群的阶一样短，为达到 80bit 安全，∣g∣=∣p∣=160|g|= |p|= 160，qq 应至少为 160 bits

3.2.7 群上的计算

  • 群的运算：给定 g,h∈Gg, h∈G，计算 g⋅hg·h

  • 群上求逆元：给定 g∈Gg∈G，计算  1/g=g−11/g=g^{-1}

    • 由 gp=g⋅gp−1=1Gg^p=g·g^{p-1}=1_G, 有 g−1=gp−1g^{-1}=g^{p-1}

  • 群上的除法：给定 g,h∈Gg, h∈G，计算 h/g=h⋅g−1h/g=h·g^{-1}

  • 群上的幂运算：给定 g∈Gg∈G 和 x∈Zpx∈Z_p，计算 gxg^x

3.3 双线性配对 Bilinear Pairings

定义

设 G1G_1，G2G_2 和 GTG_T 为素数阶为 pp 的三个循环群，则满足下述条件 e:G1×G2→GTe:G_1×G_2→G_T 的映射为一个双线性配对：

  1. (双线性) ∀x,y∈Zp,g∈G1,h∈G2∀x,y∈Z_p,g∈G_1, h∈G_2，e(gx,hy)=e(gy,hx)=e(g,h)xye(g^x,h^y)= e(g^y,h^x)=e(g,h)^{xy}

  2. (非退化性) ∀g∈G1,h∈G2,e(g,h)≠1T∀g∈G_1, h∈G_2, e(g,h)≠1_T

  3. (可计算性) ∀g∈G1,h∈G2∀g∈G_1, h∈G_2, 存在一种能计算出映射 e(g,h)e(g,h) 的高效算法

双线性配对的三种类型：

  • I 型：G1=G2G_1=G_2（对称）

  • II 型：G1≠G2G_1≠G_2，且能找到同态 ψ：G2→G1ψ ：G_2→G_1

  • III 型：G1≠G2G_1≠G_2，但没有有效的同态

3.3.1 对称配对 e:G×G→GTe:G×G→G_T

两类 DLP：

  • 从 gg 和 gxg^x 计算 xx

  • 从 e(g,g)e(g,g) 和 e(g,g)xe(g,g)^x 计算 xx
    为保证 80bit 安全，需要 ∣g∣≥512,∣e(g,g)∣≥1024|g| ≥ 512, |e(g, g)| ≥ 1024

3.3.2 非对称配对 e:G1×G2→GTe:G_1×G_2→G_T

三类 DLP：

  • 从 g1g_1 和 g1xg_1^x 计算 xx

  • 从 g2g_2 和 g2xg_2^x 计算 xx

  • 从 e(g1,g2)e(g_1,g_2) 和 e(g1，g2)xe(g_1，g_2)^x 计算 xx
    为保证 80bit 安全，需要 ∣g1∣≥160,∣g2∣≥1024,∣e(g1,g2)∣≥1024|g_1 | ≥ 160, |g_2 | ≥ 1024, |e(g_1,g_2)| ≥ 1024
    构造非对称配对时，还需注意以下问题：

  • 由于非对称结构，需设置 ∣g2∣=∣e(g1,g2))∣|g_2 | = |e(g_1,g_2))|

  • 椭圆曲线由基于配对的密码学 （PBC） 库中的 Curve-F 专门定义，其中 y2=x3+by^2=x^3+b 和 k=12k=12

3.3.3 双线性配对群上的计算

双线性配对群由素数阶 pp 的群 (G,GT)(G,G_T) 或 (G1,G2,GT)(G_1,G_2,G_T) 和双线性映射 ee 组成，其计算包括：

  • 所有在域 ZpZ_p 上的模（幂）运算

  • 对群 (G,GT)(G,G_T) 或 (G1,G2,GT)(G_1,G_2,G_T) 上的所有运算

  • ∀u,v∈G∀ u, v ∈ G 的双线性配对 e(u,v)e(u, v)

3.4 哈希函数 Hash Functions

哈希函数将任意长度的字符串作为输入，并返回一个更短的字符串作为输出

3.4.1 哈希函数的分类

1. 根据安全定义分类

  • 单向（One-Way）哈希函数：给定一个单向哈希函数 HH 和一个输出字符串 yy，很难找到满足 y=H(x)y=H(x) 的输入 xx

  • 抗碰撞（Collision-Resistant）哈希函数：给定一个抗碰撞哈希函数 HH，很难找到两个不同的输入 x1x_1 和 x2x_2 满足 H(x1)=H(x2)H(x_1 )=H(x_2)

2. 根据输出空间分类

  • H:{0,1}∗→{0,1}nH: \{0, 1\}^∗→\{0, 1\}^n：输出空间是包含所有 n 位字符串的集合

    • 主要用于从密钥空间 {0,1}n\{0, 1\}^n 生成一个对称密钥，用于混合加密

  • H:{0,1}∗→ZpH: \{0, 1\}^∗→Z_p：输出空间为 {0,1,2,⋅⋅⋅,p−1}\{0, 1, 2, · · · , p-1\}，其中 pp 是群的阶

    • 主要用于将哈希值嵌入到群的指数，譬如 gH(m)g^{H(m)}

  • H:{0,1}∗→GH : \{0, 1\}^∗ → G：输出空间是一个循环群，即将输入字符串哈希映射到一个群元素

    • 仅适用于某些群，主要是对称双线性配对 G×G→GTG×G→G_T 中的群 GG 和非对称双线性配对 G1×G2→GTG_1×G_2→G_T 中的群 G1G_1

3.5 伪随机数生成器 (Pseudo) Random Number Generator

设 xx 为随机变量，w1w1、w2w2 为空间中任意两个可能的随机数，进行随机选择操作，使得 Pr⁡[x=w1]=Pr⁡[x=w2]Pr⁡[x=w_1 ]=Pr⁡[x=w_2]

1. 方案中的随机数和现实中的区别？

  • 在方案算法中，算法可以选择满足相等概率的真正随机的随机数

  • 在现实世界中，算法是使用伪随机数生成器选择伪随机数



参考资料：

[1] 安全规约导论，郭富春

相关文章：