1 格 Point Lattices
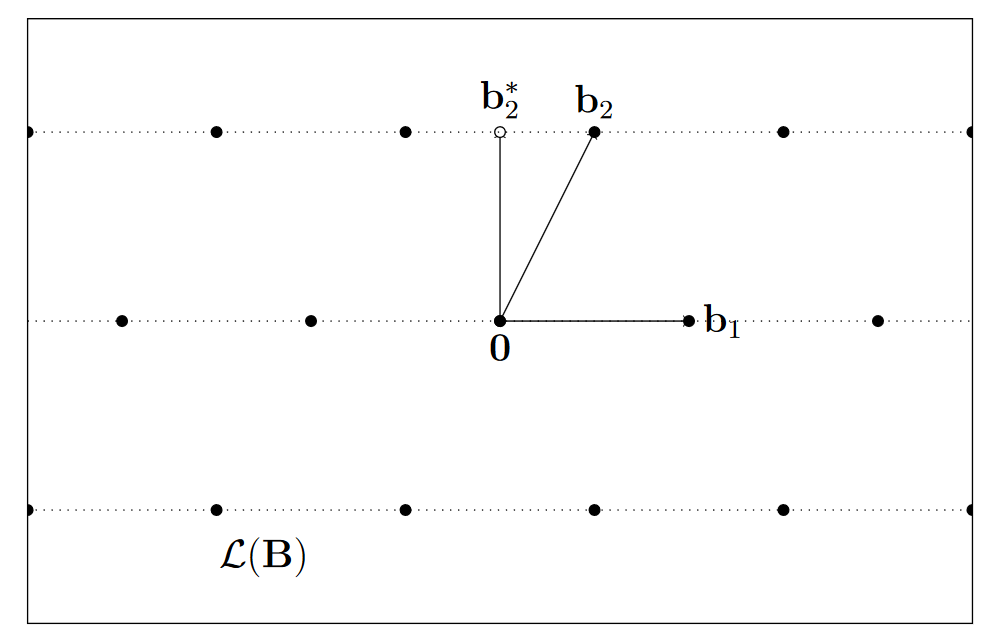
def 欧氏空间中 R n \mathbb{R}^n R n Z n \mathbb{Z}_n Z n B = [ b 1 , . . . , b n ] ∈ R d × n B=[b_1, ..., b_n] \in \mathbb{R}^{d×n} B = [ b 1 , ... , b n ] ∈ R d × n R d \mathbb{R}^d R d B B B
L ( B ) = { B x : x ∈ Z n = { ∑ i = 1 n x i ⋅ b i : ∀ i . x i ∈ Z } } \mathcal{L}(B)=\{Bx:x \in \mathbb{Z}^n =\{\sum_{i=1}^n{x_i} \cdot b_i:\forall i.x_i \in \mathbb{Z}\}\}
L ( B ) = { B x : x ∈ Z n = { i = 1 ∑ n x i ⋅ b i : ∀ i . x i ∈ Z }}
R n R^n R n B B B L ( B ) \mathcal{L}(B) L ( B ) b 1 , b 2 , . . . , b n b_1,b_2,...,b_n b 1 , b 2 , ... , b n
i.e. 格基 ( 1 , 0 ) T (1,0)^T ( 1 , 0 ) T ( 0 , 1 ) T (0,1)^T ( 0 , 1 ) T ( 1 , 1 ) T (1,1)^T ( 1 , 1 ) T ( 2 , 1 ) T (2,1)^T ( 2 , 1 ) T
n n n L ( B ) \mathcal{L}(B) L ( B ) n = d n=d n = d L ( B ) \mathcal{L}(B) L ( B )
Info
由 B B B s p a n ( B ) span(B) s p an ( B ) L ( B ) \mathcal{L}(B) L ( B ) B B B L ( B ) \mathcal{L}(B) L ( B ) s p a n ( B ) span(B) s p an ( B )
s p a n ( B ) = { B x : x ∈ R n } span(B)=\{Bx:x \in \mathbb{R}^n\}
s p an ( B ) = { B x : x ∈ R n }
1.1 子格 sublattice
def 对任意格 Λ = L ( B ) \Lambda=\mathcal{L}(B) Λ = L ( B ) Λ ′ \Lambda^{\prime} Λ ′ Λ \Lambda Λ Λ ′ ⊆ Λ \Lambda^{\prime} \subseteq \Lambda Λ ′ ⊆ Λ
2 基 Bases
def 若存在其他的矩阵 V ∈ Z n × n V \in \mathbb{Z}^{n\times n} V ∈ Z n × n V U = U V = I VU=UV=I V U = U V = I U ∈ Z n × n U \in \mathbb{Z}^{n\times n} U ∈ Z n × n
U − 1 U^{-1} U − 1 V V V U − 1 U^{-1} U − 1
G L ( n , Z ) GL(n, \mathbb{Z}) G L ( n , Z ) U − 1 U^{-1} U − 1
Note
论文中经常出现的 bases,其实是 basis 的复数形式。即当提到 “bases” 时,通常是指多组基。i.e. 两个不同的格 L ( B ) \mathcal{L}(B) L ( B ) L ( C ) \mathcal{L}(C) L ( C )
def 对矩阵 B ∈ R d × n B \in \mathbb{R}^{d \times n} B ∈ R d × n S W A P ( i , j SWAP(i, j S W A P ( i , j i ≠ j i \neq j i = j ( b i , b j ) ← ( b j , b i ) (b_i, b_j) \leftarrow (b_j, b_i) ( b i , b j ) ← ( b j , b i ) I N V E R T ( i ) INVERT(i) I N V ERT ( i ) i i i b i ← ( − b i ) b_i \leftarrow (-b_i) b i ← ( − b i ) A D D ( i , c , j ) ADD(i, c, j) A DD ( i , c , j ) i ≠ j i \neq j i = j c ∈ Z c \in \mathbb{Z} c ∈ Z b i ← ( b i + c ⋅ b j ) b_i \leftarrow (b_i + c \cdot b_j) b i ← ( b i + c ⋅ b j )
这里对矩阵的基本列操作 σ \sigma σ B B B A A A σ ( B ⋅ A ) = B − σ ( A ) \sigma(B \cdot A) = B - \sigma(A) σ ( B ⋅ A ) = B − σ ( A )
特别地,任意的基本列操作 σ \sigma σ σ ( I ) ∈ Z n × n \sigma(I) \in \mathbb{Z}^{n \times n} σ ( I ) ∈ Z n × n
σ ( B ) = σ ( B ⋅ I ) = B ⋅ σ ( I ) \sigma(B)=\sigma(B \cdot I)=B \cdot \sigma(I)
σ ( B ) = σ ( B ⋅ I ) = B ⋅ σ ( I )
由于单位矩阵 I I I B B B σ = [ σ 1 , . . . , σ k ] \sigma = [ \sigma_1, . . . , \sigma_k] σ = [ σ 1 , ... , σ k ] σ ( I ) = σ 1 ( I ) ⋅ σ 2 ( I ) . . . σ k ( I ) ∈ G L ( n , Z ) \sigma(I) = \sigma_1(I) \cdot \sigma_2(I) ... \sigma_k(I) \in GL(n, \mathbb{Z}) σ ( I ) = σ 1 ( I ) ⋅ σ 2 ( I ) ... σ k ( I ) ∈ G L ( n , Z ) L ( B ) = L ( σ ( B ) ) \mathcal{L}(B) = \mathcal{L}(\sigma(B)) L ( B ) = L ( σ ( B )) B B B σ ( B ) \sigma(B) σ ( B ) U ∈ G L ( n , Z ) U \in GL(n, \mathbb{Z}) U ∈ G L ( n , Z ) B B B
def 若∣ d e t ( B ) ∣ = 1 \left|det(B)\right|=1 ∣ d e t ( B ) ∣ = 1 B ∈ Z n × n B \in \mathbb{Z}^{n \times n} B ∈ Z n × n
lem 任意 U ∈ G L ( n , Z ) U \in GL(n, \mathbb{Z}) U ∈ G L ( n , Z )
埃尔米特形式 (Hermite normal form, HNF)的整数矩阵:i.e. 一个上三角矩阵,其中正对角元素 h i , i > 0 h_{i,i} > 0 h i , i > 0 0 ≤ h i , j < h i , i 0 ≤ h_{i,j} < h_{i,i} 0 ≤ h i , j < h i , i h i , i h_{i,i} h i , i
theo 对任意一个满秩(nonsingular)的整数方阵 B ∈ Z n × n B \in \mathbb{Z}^{n \times n} B ∈ Z n × n σ \sigma σ σ ( B ) \sigma(B) σ ( B )
coro 对任意矩阵 U ∈ Z n × n U \in \mathbb{Z}^{n \times n} U ∈ Z n × n σ \sigma σ U = σ ( I ) U = \sigma(I) U = σ ( I ) U U U U ∈ G L ( n , Z ) U \in GL(n, \mathbb{Z}) U ∈ G L ( n , Z ) U U U d e t ( U ) = ± 1 det(U)=\pm1 d e t ( U ) = ± 1
3 施密特正交化 Gram-Schmidt orthogonalization
def 通过将每一个向量投影其他向量的空间维度上,使得这组线性无关的向量 b 1 , b 2 , . . . , b n b_1,b_2,...,b_n b 1 , b 2 , ... , b n b 1 ∗ , b 2 ∗ , . . . , b n ∗ b_1^*,b_2^*,...,b_n^* b 1 ∗ , b 2 ∗ , ... , b n ∗
b i ∗ = b i ⊥ [ b 1 , . . . , b i − 1 ] b_i^*=b_i\bot[b_1,...,b_{i-1}]
b i ∗ = b i ⊥ [ b 1 , ... , b i − 1 ]
π i \pi_i π i i i i i − 1 i-1 i − 1 b i ∗ = π i ( b i ) b_i^*=\pi_i(b_i) b i ∗ = π i ( b i ) B ∗ B^* B ∗ L ( B ) \mathcal{L} (B) L ( B ) B ∗ B^* B ∗ b 1 , b 2 , . . . , b n b_1,b_2,...,b_n b 1 , b 2 , ... , b n b 1 ∗ , b 2 ∗ , . . . , b n ∗ b_1^*,b_2^*,...,b_n^* b 1 ∗ , b 2 ∗ , ... , b n ∗ b 1 = ( 2 , 0 ) b_1=(2,0) b 1 = ( 2 , 0 ) b 2 = ( 1 , 2 ) b_2=(1,2) b 2 = ( 1 , 2 ) [ b 1 , b 2 ] [b_1,b_2] [ b 1 , b 2 ] b 1 ∗ = b 1 , b 2 ∗ = b 2 ⊥ b 1 = ( 1 , 2 ) b_1^*=b_1, b_2^*=b_2 \bot b_1=(1,2) b 1 ∗ = b 1 , b 2 ∗ = b 2 ⊥ b 1 = ( 1 , 2 ) b 2 ∗ b_2^* b 2 ∗ L ( B ) \mathcal{L}(B) L ( B ) [ b 2 , b 1 ] [b_2,b_1] [ b 2 , b 1 ] b 2 ∗ = b 2 , b 1 ∗ = b 1 ⊥ b 2 = ( 8 5 , − 4 5 ) b_2^*=b_2, b_1^*=b_1 \bot b_2=(\frac{8}{5},-\frac{4}{5}) b 2 ∗ = b 2 , b 1 ∗ = b 1 ⊥ b 2 = ( 5 8 , − 5 4 )
B = [ b 1 , b 2 , . . . , b n ] B=[b_1,b_2,...,b_n] B = [ b 1 , b 2 , ... , b n ]
b i ∗ = b i − ∑ j < i μ i , j b j ∗ w h e r e μ i , j = ⟨ b i , b j ∗ ⟩ ⟨ b j ∗ , b j ∗ ⟩ b_i^*=b_i-\sum_{j < i}{\mu_{i, j}b_j^* \: where \: \mu_{i, j}=\frac{\langle b_i, b_j^*\rangle}{\langle b_j^*,b_j^*\rangle}}
b i ∗ = b i − j < i ∑ μ i , j b j ∗ w h ere μ i , j = ⟨ b j ∗ , b j ∗ ⟩ ⟨ b i , b j ∗ ⟩
B B B B ∗ B^* B ∗ B = B ∗ T B=B^*T B = B ∗ T T = [ 1 μ 2 , 1 ⋯ μ n , 1 ⋱ ⋮ 1 μ n , n − 1 1 ] T=\begin{bmatrix} 1 & \mu_{2,1} & \cdots & \mu_{n,1} \\ & \ddots & & \vdots\\ & \ & 1 & \mu_{n,n-1} \\ & & & 1\end{bmatrix} T = 1 μ 2 , 1 ⋱ ⋯ 1 μ n , 1 ⋮ μ n , n − 1 1
4 格的行列式 The determinant
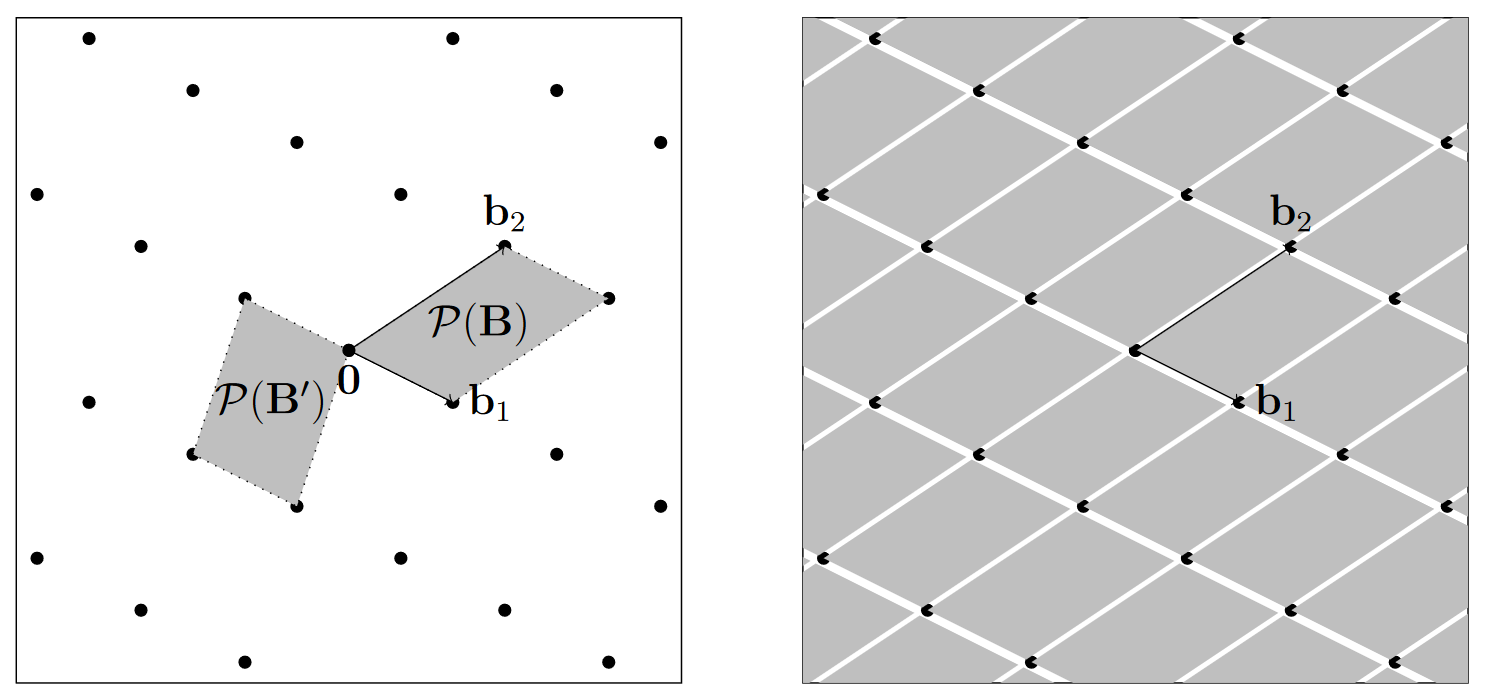
def 给定一个基 B = [ b 1 , … , b n ] ∈ R d × n B = [b_1, \dots, b_n] \in \mathbb{R}^{d \times n} B = [ b 1 , … , b n ] ∈ R d × n P ( B ) = B T n = { ∑ i = 1 n x i ⋅ b i ∣ ∀ i , 0 ≤ x i < 1 } P(B) = B \mathbb{T}^n = \left\{ \sum_{i=1}^{n} x_i \cdot b_i \mid \forall i, 0 \leq x_i < 1 \right\} P ( B ) = B T n = { ∑ i = 1 n x i ⋅ b i ∣ ∀ i , 0 ≤ x i < 1 } T = [ 0 , 1 ) \mathbb{T}= [0, 1) T = [ 0 , 1 )
P ( B ) P(B) P ( B ) [ 0 , 1 ) [0,1) [ 0 , 1 ) Λ \Lambda Λ span ( Λ ) \text{span}(\Lambda) span ( Λ ) x ∈ Λ x \in \Lambda x ∈ Λ S S S { x + S : x ∈ Λ } \{x + S : x \in \Lambda\} { x + S : x ∈ Λ } span ( Λ ) \text{span}(\Lambda) span ( Λ ) S ⊂ span ( Λ ) S \subset \text{span}(\Lambda) S ⊂ span ( Λ )
分割(partition):S S S x + S x + S x + S span ( Λ ) \text{span}(\Lambda) span ( Λ )
Note
格基本区的其他分割方式:
正交(orthogonalized)平行多面体 P ( B ∗ ) P(B^*) P ( B ∗ )
中心(centered)平行多面体 C ( B ) C(B) C ( B ) P ( B ) P(B) P ( B ) − 1 2 ∑ i = 1 n b i -\frac{1}{2} \sum_{i=1}^n b_i − 2 1 ∑ i = 1 n b i
C ( B ) = B ⋅ [ − 1 2 , 1 2 ) n = − 1 2 ∑ i = 1 n b i + P ( B ) C(B) = B \cdot \left[-\frac{1}{2}, \frac{1}{2}\right)^n = -\frac{1}{2} \sum_{i=1}^n b_i + P(B)
C ( B ) = B ⋅ [ − 2 1 , 2 1 ) n = − 2 1 i = 1 ∑ n b i + P ( B )
正交中心平行多面体 C ( B ∗ ) C(B^*) C ( B ∗ ) P ( B ∗ ) 平移 − 1 2 ∑ i = 1 n b i ∗ P (B^*) 平移 -\frac {1}{2} \sum_{i=1}^n b_i^* P ( B ∗ ) 平移 − 2 1 ∑ i = 1 n b i ∗
C ( B ∗ ) = B ∗ ⋅ [ − 1 2 , 1 2 ) n = − 1 2 ∑ i = 1 n b i ∗ + P ( B ∗ ) C(B^*) = B^* \cdot \left[-\frac{1}{2}, \frac{1}{2}\right)^n = -\frac{1}{2} \sum_{i=1}^n b_i^* + P(B^*)
C ( B ∗ ) = B ∗ ⋅ [ − 2 1 , 2 1 ) n = − 2 1 i = 1 ∑ n b i ∗ + P ( B ∗ )
def 给定一个基 B ∈ R d × n B\in R^{d \times n} B ∈ R d × n B ∗ B^* B ∗ Λ = L ( B ) \Lambda = \mathcal{L}(B) Λ = L ( B ) B B B
det ( Λ ) = vol ( P ( B ) ) = ∏ i ∥ b i ∗ ∥ \det(\Lambda) = \text{vol}(P(B)) = \prod_i \|b^*_i\|
det ( Λ ) = vol ( P ( B )) = i ∏ ∥ b i ∗ ∥
格的行列式等于格的基本区体积,且与所选择的基无关。即无论选择哪个基 B B B det ( Λ ) \det(\Lambda) det ( Λ )
行列式可以看作是空间中格点密度的倒数。对格 Λ \Lambda Λ det ( Λ ) \det(\Lambda) det ( Λ ) A A A A A A b 1 , b 2 ∈ R 2 b_1,b_2 \in \mathbb{R}^2 b 1 , b 2 ∈ R 2 ∥ b 1 ∥ = 2 \|b_1\| = 2 ∥ b 1 ∥ = 2 ∥ b 2 ∥ = 3 \|b_2\| = 3 ∥ b 2 ∥ = 3 R 2 \mathbb{R}^2 R 2 Λ \Lambda Λ det ( Λ ) = 2 × 3 = 6 \det(\Lambda)=2 \times 3=6 det ( Λ ) = 2 × 3 = 6 A A A A A A 60 6 = 10 \frac{60}{6} = 10 6 60 = 10
theo 阿达马不等式(Hadamard Inequality)对于任何格 Λ = L ( B ) \Lambda = \mathcal{L}(B) Λ = L ( B ) det ( Λ ) \det(\Lambda) det ( Λ )
det ( Λ ) ≤ ∏ i ∥ b i ∥ \det(\Lambda) \leq \prod_{i} \|b_i\|
det ( Λ ) ≤ i ∏ ∥ b i ∥
上界 ∥ b i ∗ ∥ ≤ ∥ b i ∥ \|b_i^*\| \leq \|b_i\| ∥ b i ∗ ∥ ≤ ∥ b i ∥ b i ∗ b_i^* b i ∗ b i b_i b i b i ∗ b_i^* b i ∗
正交基的平行多面体体积最大,因此行列式 det ( Λ ) \det(\Lambda) det ( Λ )
lem 对于任何格基 B ∈ R d × n B \in \mathbb{R}^{d \times n} B ∈ R d × n Λ = L ( B ) \Lambda = \mathcal{L}(B) Λ = L ( B )
det ( Λ ) = det ( B T B ) \det(\Lambda) = \sqrt{\det(B^T B)}
det ( Λ ) = det ( B T B )
特别地,如果 B B B n × n n \times n n × n
det ( Λ ) = ∣ det ( B ) ∣ \det(\Lambda) = |\det(B)|
det ( Λ ) = ∣ det ( B ) ∣
为了在 P P T PPT PPT p 1 , p 2 , … , p k p_1, p_2, \dots, p_k p 1 , p 2 , … , p k det ( B ) \det(B) det ( B ) p i p_i p i det ( B ) m o d p i \det(B)\mod p_i det ( B ) mod p i det ( B ) \det(B) det ( B )
对基 B B B B T B B^TB B T B
当 B B B
theo 假设 B B B C C C Λ \Lambda Λ Λ ( B ) = Λ ( C ) \Lambda(B) = \Lambda(C) Λ ( B ) = Λ ( C ) v o l ( P ( B ) ) = v o l ( P ( C ) ) vol(P(B))=vol(P(C)) v o l ( P ( B )) = v o l ( P ( C ))
注:
参考格密码的基础概念(1) 如何通俗地理解施密特正交化|马同学图解线性代数
![]()