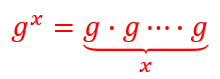Hyper の 个人博客

1 对象存活判定算法

1.1 引用计数器

def （使用较少）经引用变量操作，判断对象是否还有使用价值

• 每个对象都包含一个 引用计数器，用于存放被引用的计数

• 每当有一个地方引用此对象时，引用计数 +1；当引用失效时，引用计数 -1

  • i.e. 当前离开了局部变量的作用域，引用计数 -1
  • i.e. 引用被设为 null 时，引用计数 -1

• 当引用计数为 0 时，表示此对象为不可能再被使用的已死对象，即已无任何方法得到该对象的引用

1
2
3
4
5
6
7
8
9
10
11
12
13

public class Main {
    public static void main(String[] args) {
        Test a = new Test();
        Test b = new Test();
        a.another = b;
        b.another = a;
        a = b = null;
    }
    
    private static class Test {
        Test another;
    }
}

1.2 可达性分析算法

def （主流 JVM 采用）类似树结构的搜索机制，用于判断对象是否存活。每个对象的引用都有机会成为树的根节点 (GC Roots) 节点，条件如下：

• 位于虚拟机栈的栈帧中的本地变量表中所引用到的对象（i.e. 方法中的局部变量），同样也包括本地方法栈中 JNI 引用的对象。

• 类的静态成员变量引用的对象

• 方法区中常量池引用的对象，i.e. String 类型对象

• 被添加了锁的对象，i.e. synchronized 修饰的对象

• 虚拟机内部需要使用的对象

则对于之前的问题，由于 GCRoots 已被回收，虽然 a、b 两对象之间仍存在相互引用，但由于两者跟 GCRoots 均无关联，故此时 a、b 均会被 GC 回收

1.3 Java 引用类型

def （JDK1.2 前）如果 reference 类型的数据中，存储的数值代表的是另外一块内存的起始地址，就称该 reference 数据是代表某块内存、某个对象的引用。（JDK1.2 及之后）Java 将引用的概念扩充至下述四种类型（引用强度依次递减）：

• 强引用（Strong Reference）：即传统定义上的引用，被强引用关联的对象不会被回收

1

Object obj = new Object();

• 软引用（Soft Reference）：有用但非必须的对象，只被软引用关联着的对象，在系统将要发生内存溢出异常前，会把这些对象列进回收范围之中进行第二次回收，如果这次回收还没有足够的内存，才会抛出内存溢出异常

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

// 添加虚拟机选项-XX:+PrintGCDetails -Xms10M -Xmx10M
Object obj = new Object();
ReferenceQueue<Object> q = new ReferenceQueue<>();
SoftReference<Object> sf = new SoftReference<>(obj, q);
// 取消强引用绑定关系
obj = null;
System.out.println(sf.get());
try {
    List<String> li = new ArrayList<>();
    while (true) {
        li.add("newObj");
    }
} catch (Throwable t) {
    /*
    发生内存溢出: Java heap space
    当前软引用对象: null
    指向被GC回收对象的引用: java.lang.ref.SoftReference@4554617c
    */
    System.out.println("发生内存溢出: " + t.getMessage());
    System.out.println("当前软引用对象: " + sf.get());
    System.out.println("指向被GC回收对象的引用: " + q.poll());
}

• 弱引用（Weak Reference）：非必须对象，被弱引用关联的对象只能生存到下一次 GC 发生为止，即只要进行 GC 一定回收

1
2
3
4
5
6
7

WeakReference<Object> wf = new WeakReference<>(new Object());
// Output: java.lang.Object@1b6d3586
System.out.println(wf.get());
// 手动发起GC
System.gc();
// Output: null
System.out.println(wf.get());

• 虚引用（Phantom Reference）：虚引用关联的对象会在被收集器回收时收到一个系统通知（仅此而已），该对象在任何情况下都可能被回收。虚引用与对象的存活时间无关，且无法通过虚引用得到关于对象的一个实例

1
2
3
4
5

ReferenceQueue<Object> q = new ReferenceQueue<>();
// 只能使用带队列的构造方法
PhantomReference<Object> pf = new PhantomReference<>(new Object(), q);
// Output: null
System.out.println(pf.get());

1.4 对象死亡判定

要真正宣告一个对象死亡，至少要经历两次标记过程：

• 若对象进行可达性分析后，没有与 GC Roots 相连接的引用链，将被第一次标记并筛选，筛选条件为此对象是否有必要执行 finalize() 方法

  • 对象没有覆盖 finalize() 方法：无需执行
  • finalize() 方法已经被虚拟机调用过：无需执行

• 若有必要执行，则将对象放入 F-Queue，并在稍后交由一个虚拟机自己建立的、低优先级的 Finalizer 线程执行；稍后 GC 将对 F-Queue 中的对象进行第二次小规模的标记，仍未被引用的对象会被回收

1.4.1 finalize () 方法

1
2

// 一般用于释放对象的一些额外资源，目前已不推荐使用，相比cpp的析构函数运行代价过大
protected void finalize() throws Throwable { }

• finalize ()：对象的最终判定方法，若子类重写了该方法，会先暂时进入 F-Queue 队列，并在 GC 判定子类对象为可回收时，进行二次确认。

  • 不由主线程执行，而是由 VM 创建的低优先级的 Finalizer 线程
  • 对每个对象 finalize () 只能生效 1 次。下一次 GC 进行回收时，不会再次调用此方法

• 此方法执行过程中，当前对象可重新建立 GCRoots，即可不被回收，并从 F-Queue 队列中移除。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public class Main {
    private static Test a;
    
    public static void main(String[] args) throws InterruptedException {
        a = new Test();
        // 置为null，此时与GCRoots的关联断开
        a = null;
        // 手动申请GC回收
        System.gc();
        
        Thread.sleep(1000);
        
        // 此时经二次确认后，a仍不会被GC回收
        System.out.println(a);
    }
    
    private static class Test {
        @Override
        protected void finalize() throws Throwable {
            System.out.println(this);
            a = this;
        }
    }
}

1.5 方法区的回收

由于方法区回收的性价比较低，java 虚拟机规范中未强制要求对方法区实现垃圾收集（i.e. JDK 11 时期的 ZGC 收集器就不支持类卸载）。在大量使用反射、动态代理、CGLib 等字节码框架，动态生成 JSP 以及 OSGi 这类频繁自定义类加载器的场景中，通常需要 JVM 具备类型卸载的能力，以保证不会对方法区造成过大的内存压力。方法区（永久代）主要回收两部分内容：

• 废弃常量

  • e.g. 常量池中字面量回收：字符串 “java” 曾进入常量池中，但当前系统又没有任何一个字符串对象的值是 “java”，即无任何字符串对象引用常量池中的 “java” 常量、虚拟机中也没有其他地方引用这个字面量，此时若发生垃圾回收，垃圾收集器在判断确有必要的情况下，会将 “java” 常量清理出常量池

• 无用的类：-Xnoclassgc 参数控制是否对类进行卸载。判定一个类型是否属于不再被使用的类，需同时满足：

  • 该类所有的实例都已经被回收，即 Java 堆中不存在该类的任何实例
  • 加载该类的 ClassLoader 已经被回收（通常很难达成）
  • 该类对应的 java.lang.Class 对象没有在任何地方被引用，无法在任何地方通过反射访问该类的方法

2 垃圾回收算法

2.1 分代收集机制

2.1.1 Java 堆内存的划分

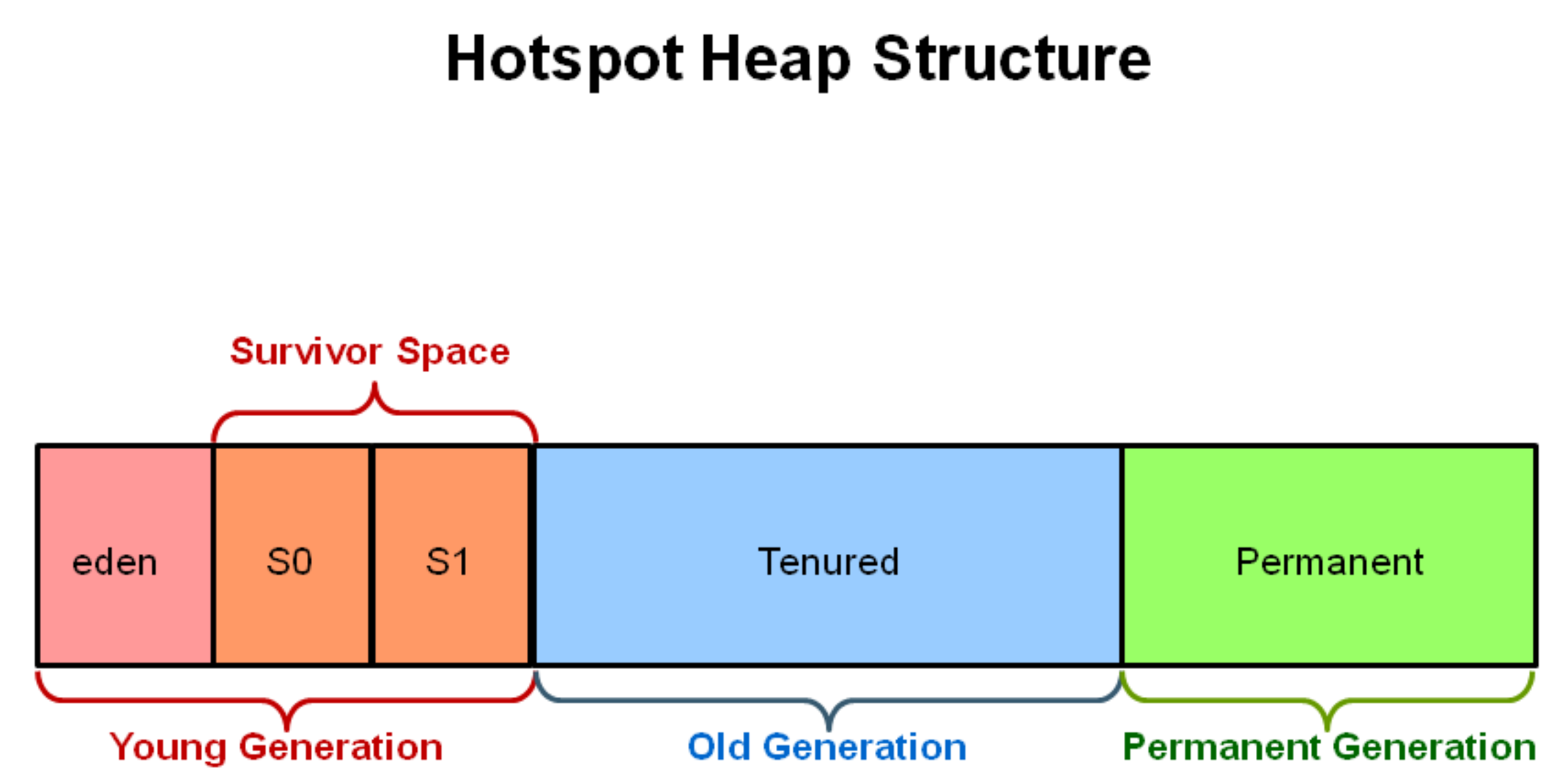
新生代、老年代和永久代

• 区分：JDK8 前方法区采用永久代实现，JDK8 后为元空间，使用本地内存

• 新生代 = Eden + Survivor ($S_0$) + Survivor ($S_1$)，默认比例 8 : 1 : 1

• GC 频率：新生代 ＞ 老年代 ＞ 永久代

2.1.2 垃圾回收策略

• 新生代的垃圾回收过程：次要垃圾回收（ Young GC / Minor GC）

  • Trigger：Eden 区满

• 老年代的垃圾回收过程：主要垃圾回收（Old GC / Major GC）

  • 只有 CMS GC 有单独收集老年代的行为

• 对整个 Java 堆内存和方法区进行垃圾回收：完全垃圾回收（Full GC）

  • Trigger 1：老年代剩余空间不足，每次晋升到老年代的对象平均大小大于老年代剩余空间
  • Trigger 2：老年代剩余空间不足，Minor GC 后新生代存活的对象超过老年代剩余空间
  • *Trigger 3：永久代空间不足（JDK8 前）
  • Trigger 4：手动调用 System.gc() 方法
  • *Trigger 5：老年代剩余空间不足，CMS GC 过程中同时有对象要放入老年代，而此时 GC 过程中浮动垃圾过多导致暂时性的空间不足，便会报 Concurrent Mode Failure 错误并触发 Full GC

• * 对新生代和部分老年代进行垃圾回收：混合垃圾回收（Mixed GC）

  • 只有 G1 GC 有这种行为

2.1.3 Minor GC 的基本原理

假设此时 Survivor ($S_0$) 为 From 区，Survivor ($S_1$) 为 To 区，有：

• Step 1：新创建的小对象进入新生代的 Eden 区、大对象直接进入老年代。

• Step 2：Eden 区满时，JVM 会触发一次 Minor GC，对新生代区域内所有对象进行扫描，在 Eden 区和 Survivor 区中的对象会进行存活性分析，无法达到存活条件的对象会被回收

• Step 3：上述过程中未被回收的对象需要被复制到新的位置：

  • 对于原来位于 Eden 区且存活的对象，复制到 To 区（$S_1$）
  • 对于原来位于 From 区（$S_0$）且存活的对象，复制到 To 区（$S_1$），且这些对象的年龄会增加 1

• Step 4：原来的 From 区（$S_0$）将被清空，Minor GC 结束，From 区和 To 区交换角色：To 区成为新的 From 区、之前的 From 区成为新的 To 区，即$S_1$变为新的 From 区，$S_0$变为新的 To 区。

• Step 5：重复上述步骤。如果某个对象的年龄达到一定的阈值，该对象从 To 区晋升到老年代，不再在新生代中移动

2.1.4 空间分配担保

Survivor 的 To 区空间是有限的。如果 Minor GC 后新生代的 Eden 区中仍存在大量的对象，就需要将一部分过多的对象晋升到老年代。工作流程如下：

• Step 1：Minor GC 前，JVM 检查最大可用的连续空间是否大于新生代所有对象总空间，即老年代的可用空间是否足够容纳即将晋升的新生代对象，并根据之前 GC 的晋升情况和新生代中对象的存活率，预估出本次 GC 可能需要晋升的对象数量

• Step 2：

  • 如果老年代有足够的空间容纳这些晋升对象，则直接进行 Minor GC
  • 如果老年代空间不足以容纳这些晋升对象，JVM 将查看 HandlePromotionFailure 设置值是否允许担保失败，如果允许那么就会继续检查老年代最大可用的连续空间是否大于历次晋升到老年代对象的平均大小，如果大于，将尝试着进行一次 Minor GC；否则，如果小于或 HandlePromotionFailure 设置不允许冒险，则将触发 Full GC，回收老年代中未使用的对象，以释放空间。在极端情况下，如果 Full GC 后老年代依然没有足够的空间，则抛出 OutOfMemoryError

• Step 3：JVM 根据多次 GC 的结果动态调整担保策略。如果新生代对象的晋升比例较低，JVM 可能在后续 Minor GC 时减少对老年代空间的需求预测；如果晋升对象过多，JVM 可能会更加保守地预留老年代空间

* 注：JDK 6 Update 24 后，-XX:HandlePromotionFailure 参数不再影响虚拟机的空间分配担保策略。只要老年代的连续空间大于新生代对象总大小 / 历次晋升的平均大小，就会进行 Minor GC；否则进行 Full GC

2.2 标记 - 清除算法

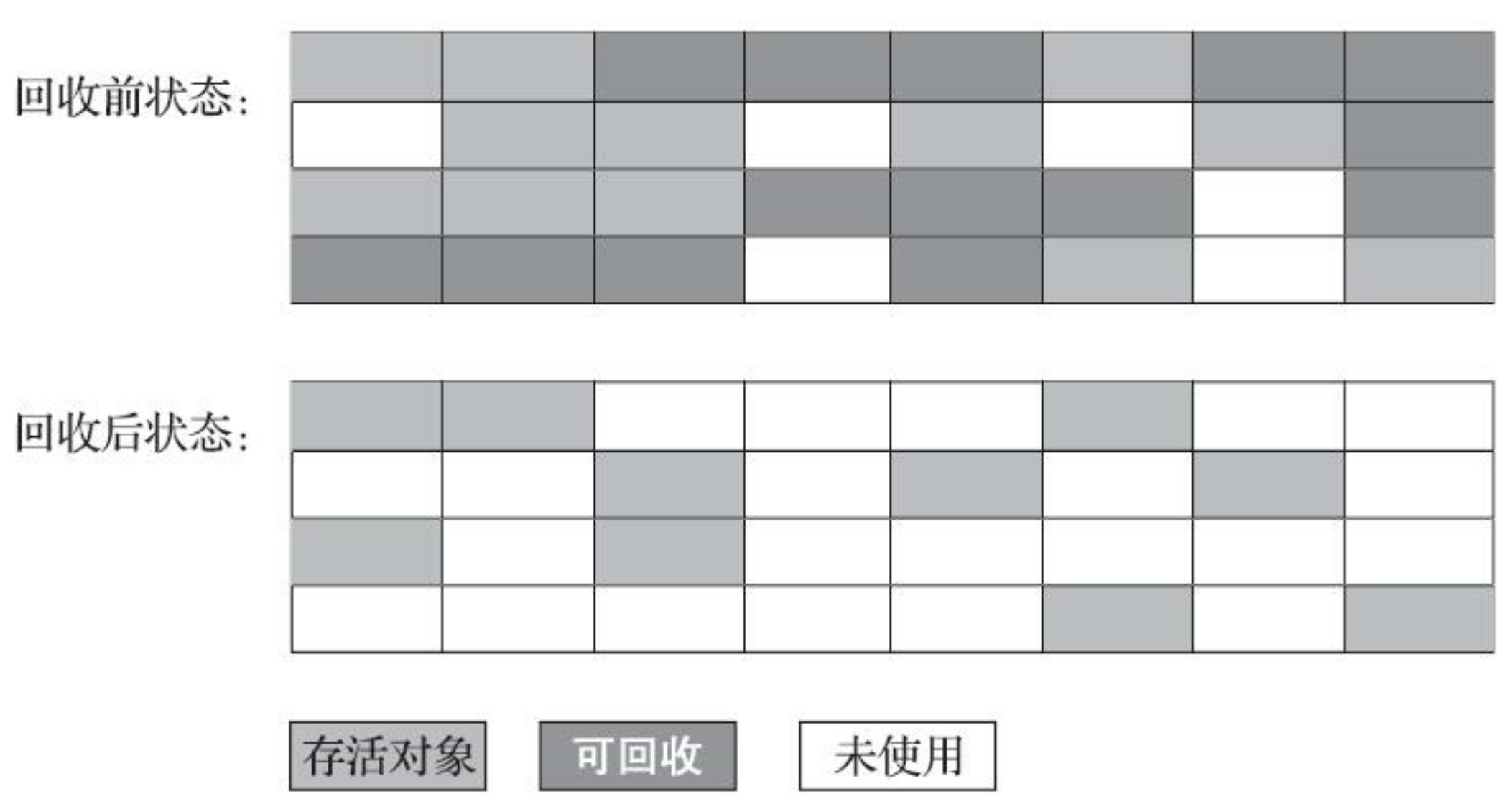
• 标记 - 清除（Mark-Sweep），有两类形式：

  • 标记出所有需回收的对象，完成后统一回收已标记的对象
  • 标记出所有仍存活的对象，完成后统一回收未标记的对象

• 缺点：

  • 执行效率不稳定：标记、清除两过程的执行速度均和内存中的对象数目成反比
  • 内存空间碎片化：这种内存分配方式会产生大量不连续的内存碎片，可能导致连续内存的空间利用率降低，i.e. 无法为大对象分配足够的连续内存

2.3 标记 - 复制算法

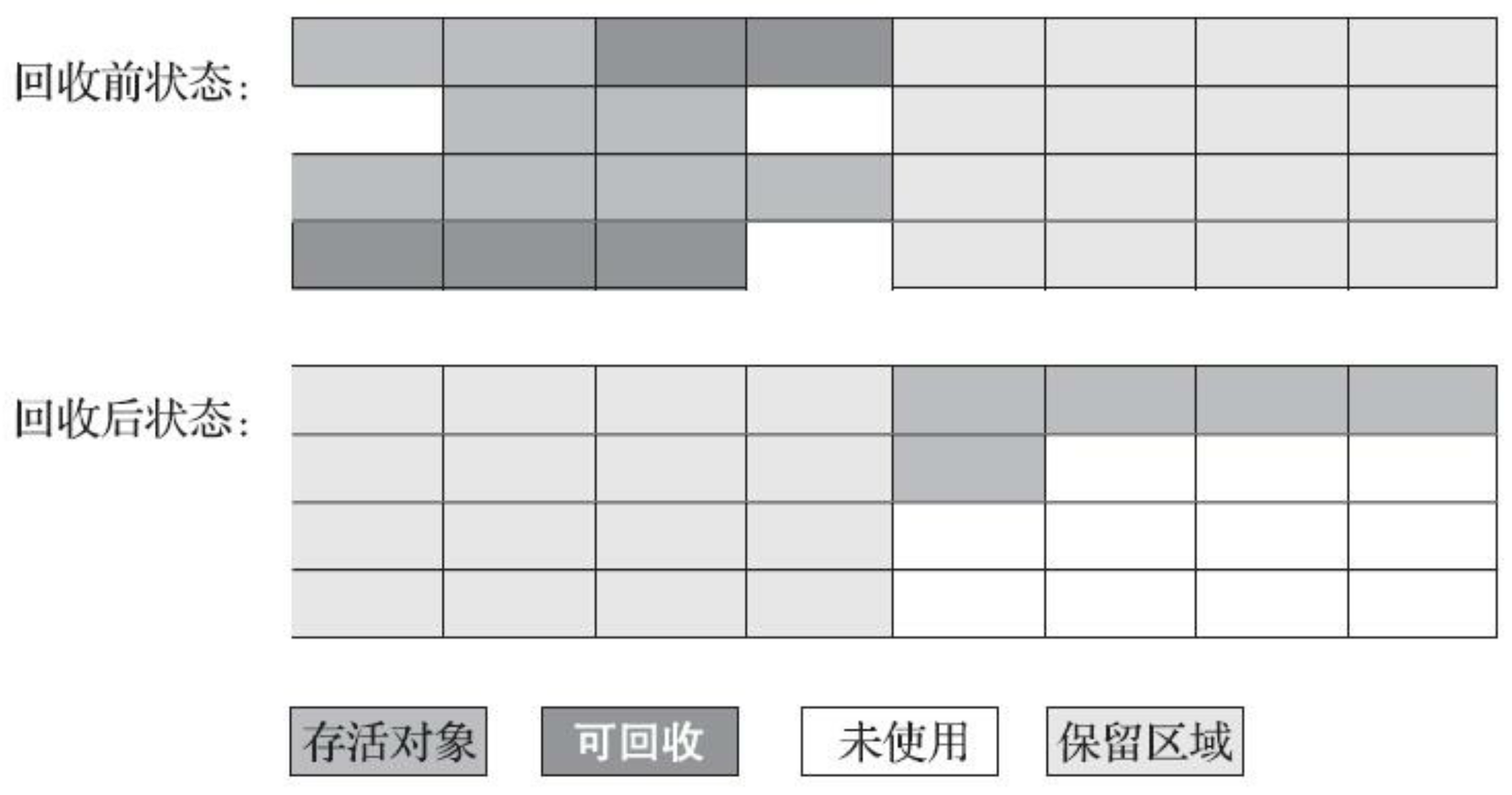
• def 半区复制（Semispace Copying）：将可用内存等分为两块，每次仅使用其中一块。当这块内存空间满时，将其中的所有存活对象复制到另一块上

• 优点：实现简单，运行高效。仅需要复制占少数的存活对象，这种内存分配方式不会产生空间碎片，每次复制时时按照堆顶指针的移动来顺序分配存活对象

• 缺点：可用内存减半

• 应用：商用 JVM 常用此方法的变种，i.e. Appel 式回收

2.4 标记 - 整理算法

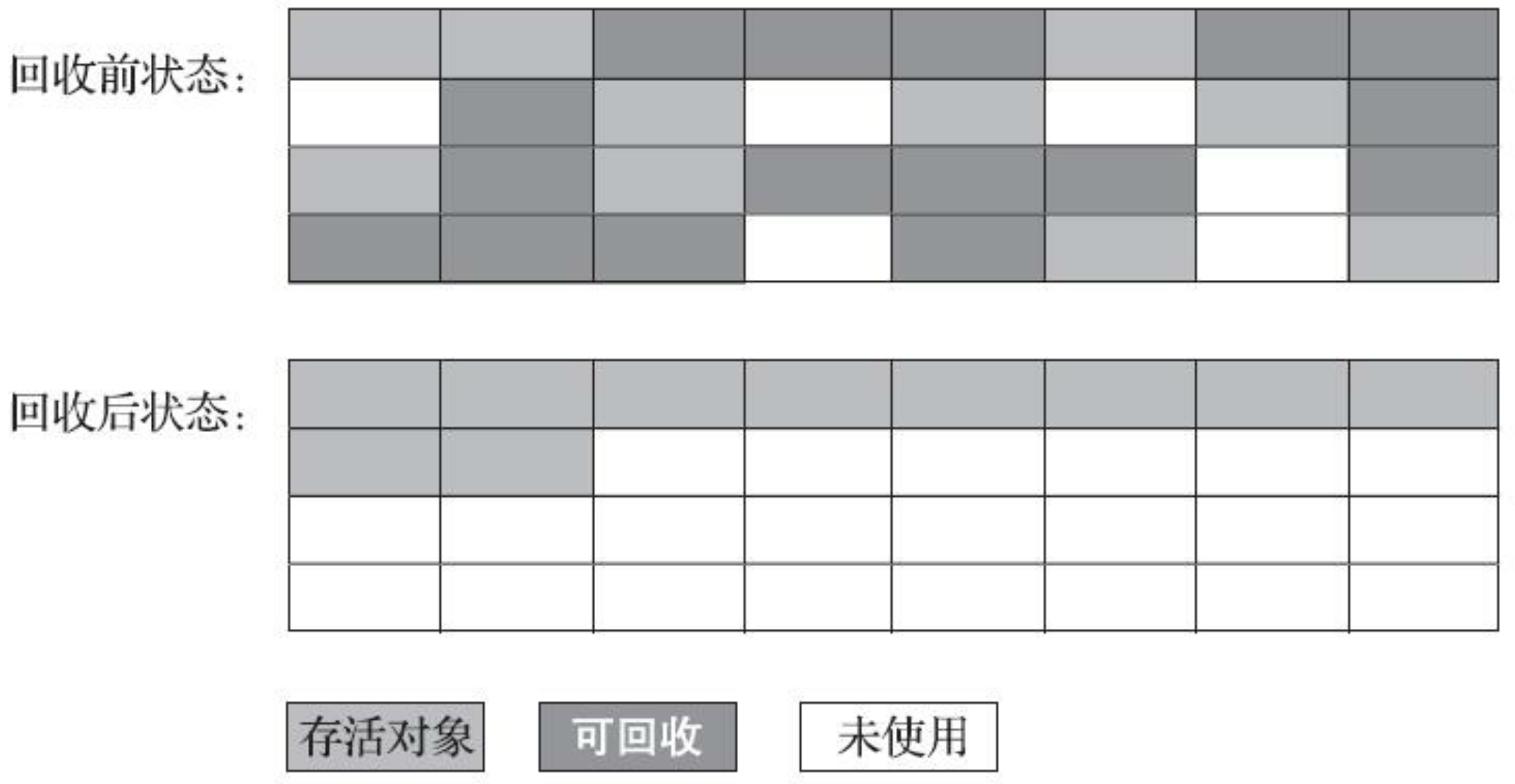
• 标记 - 整理（Mark-Compact）：针对老年代的移动式回收算法。标记出所有仍存活的对象，完成后将这些对象向内存空间一端移动（整理），并直接清理掉边界以外的内存

• 优点：内存分配和访问快，赋值器（Mutator）的吞吐量更高。赋值器为使用垃圾收集的用户程序

• 缺点：内存回收耗时增加，移动存活对象并更新所有引用较为耗时，且需全程暂停用户应用程序（“Stop The World”）才能进行

3 HotSpot 的算法实现

3.1 根节点枚举

• 目前主流 JVM 为准确式垃圾收集，因需确保在一致性的快照中进行可达性分析，GC 时必须停顿所有线程

• 在 HotSpot 的解决方案里，是使用一组称为 OopMap 的数据结构来记录存放对象引用的位置

• 一旦类加载动作完成，HotSpot 就会把对象内什么偏移量上是什么类型的数据计算出来，在 JIT 编译过程中会在特定的位置记录下栈和寄存器中哪些位置是引用，这样收集器在扫描时就可以直接得知这些信息，无需真正一个不漏地从方法区等 GC Roots 开始查找

e.g. HotSpot 虚拟机客户端模式下，生成的一段 String::hashCode () 方法的本地代码。OopMap 位于 0x026eb7a9，指明了 EBX 寄存器和栈中偏移量为 16 的内存区域中各有一个普通对象指针（Ordinary Object Pointer，OOP）的引用，有效范围为从 call 指令开始直到 0x026eb730（指令流的起始位置）+142（OopM ap 记录的偏移量)=0x026eb7be，即 hlt 指令为止

3.2 安全点

def HotSpot 没有为每条指令都生成 OopMap，而是只在特定位置记录了这些信息，这些位置称为安全点

• 程序执行时，只有到达安全点时才能暂停并开始 GC

• 安全点的选取：是否具有让程序长时间执行的特征，e.g. 方法调用、循环跳转、异常跳转

在 GC 前让所有线程跑到安全点的方法：

• 抢先式中断（Preemptive Suspension，几乎不使用）：系统首先中断全部用户线程，将不在安全点上中断的用户线程恢复执行，直到跑到安全点上后重新中断

• 主动式中断（Voluntary Suspension）：不直接对线程操作，仅设置一个标志位（与安全点重合，加上创建对象分配内存的地方），各个线程执行时会不停地主动去轮询这个标志，一旦发现中断标志为真时就自己在最近的安全点上主动中断挂起

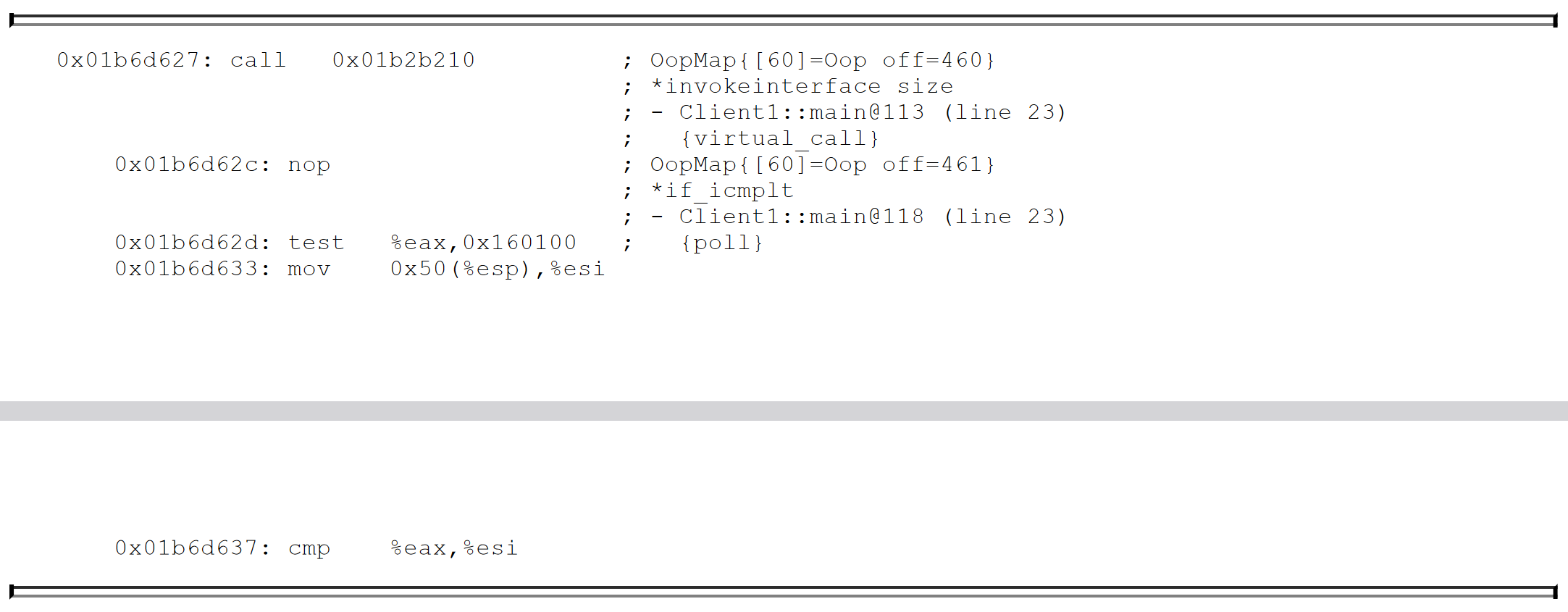
e.g. 由于轮询操作在代码中频繁出现，HotSpot 使用内存保护陷阱的方式，把轮询操作精简至只有一条汇编指令。当需要暂停用户线程时，虚拟机把 0x160100 的内存页置为不可读，线程执行到 test 指令时就会产生一个自陷异常信号，然后在预先注册的异常处理器中挂起等待，完成安全点轮询并触发线程中断

3.3 安全区域

def 用户线程处于 Sleep/Blocked 状态时，无法响应虚拟机的中断请求，无法走到安全点再中断；需要确保在某一段代码片段之中的引用关系不会发生变化，即在这个区域中任意地方开始 GC 都是安全的，这个区域称为安全区域

• 当用户线程执行到安全区域中的代码时，首先会标识进入了安全区域，虚拟机 GC 时不会处理已声明在安全区域内的线程

• 当线程将要离开安全区域时，将检查虚拟机是否已经完成了根节点枚举（或垃圾收集过程中其他需要暂停用户线程的阶段），若完成则继续执行；否则，等待直到收到离开安全区域的信号为止

3.4 记忆集与卡表

def 记录集是记录从非收集区域指向收集区域的指针集合的抽象数据结构，用于缩减 GC Roots 扫描范围

1
2
3
4

// 用非收集区域中所有含跨代引用的对象数组实现
Class RememberedSet {
    Object[] set[OBJECT_INTERGENERATIONAL_REFERENCE_SIZE];
}

上述方式记录了非收集区域中的所有含跨代引用对象，维护成本较高；而通过记忆集，只需判断某一块非收集区域是否存在指向收集区域的指针，无需了解这些跨代指针的全部细节。记忆集有三类主流设计思路：

• 字长精度：每个记录精确到一个机器字长（处理器的寻址位数，i.e. 32/64 位，该精度决定机器访问物理内存地址的指针长度），该字包含跨代指针

• 对象精度：每个记录精确到一个对象，该对象里有字段含有跨代指针

• 卡精度：每个记录精确到一块内存区域，该区域内有对象含有跨代指针

  • 使用卡表（Card Table）实现，其中的每个元素对应其标识的内存区域中一块特定大小（i.e. 如下为 512 字节）的内存块，称卡页（Card Page）
  • 单个卡页中常包含多个对象，存在两类情况：（1）至少一个对象的字段中存在跨代指针，将卡页的标识置为 1，称为这个元素变脏（Dirty），当前卡页称为脏卡，将于 GC 时被加入 GC Roots 中一并扫描；（2）若不存在跨代指针，则标识为 0

1
2

// HotSpot虚拟机中，卡表为一个字节数组
CARD_TABLE[this address >> 9] = 0;

3.5 写屏障

def 写屏障是在其他分代区域对象引用本区域对象并赋值时，用于维护卡表的操作。基本流程包括：

• 其他分代区域对象引用本区域对象，赋值时产生一个环形（Around）通知，供程序执行额外的动作

• 写前屏障（Pre-Write Barrier）：顾名思义，在赋值前进行

• 写后屏障（Post-Write Barrier）：更常用，G1 以前的收集器均只使用写后屏障

1
2
3
4
5
6

void oop_field_store(oop* field, oop new_value) {
    // 1. 引用并赋值
    *field = new_value;
    // 2. 写后屏障更新卡表
    post_write_barrier(field, new_value);
}

1
2
3

if (CARD_TABLE [this address >> 9] != 0) {
	CARD_TABLE [this address >> 9] = 0;
}

3.6 并发的可达性分析

3.6.1 三色标记（Tri-color Marking）

• 白色：尚未被垃圾收集器访问过的对象

  • 可达性分析开始时，所有对象均为白色
  • 分析结束时，仍为白色的对象是不可达的

• 黑色：已经被 GC 访问过、所有引用均已扫描过的对象

  • 黑色的对象是安全存活的
  • 如果有其他对象引用指向黑色对象，则无须重新扫描一遍
  • 黑色对象不可能直接（不经过灰色对象）指向某个白色对象

• 灰色：已被 GC 访问过、至少存在一个引用未被扫描过的对象

3.6.2 “对象消失” 问题

def 用户线程与收集器并发工作，收集器在对象图上标记颜色，同时用户线程在修改引用关系（修改对象图的结构），则会导致两种后果：

• 把原本消亡的对象错误标记为存活：可容忍的，下次 GC 时清理

• 把原本存活的对象错误标记为已消亡：严重，会导致程序出错，即对象消失问题

  • 情况 1：赋值器插入了一条或多条从黑色对象到白色对象的新引用
  • 情况 2：赋值器删除了全部从灰色对象到该白色对象的直接或间接引用

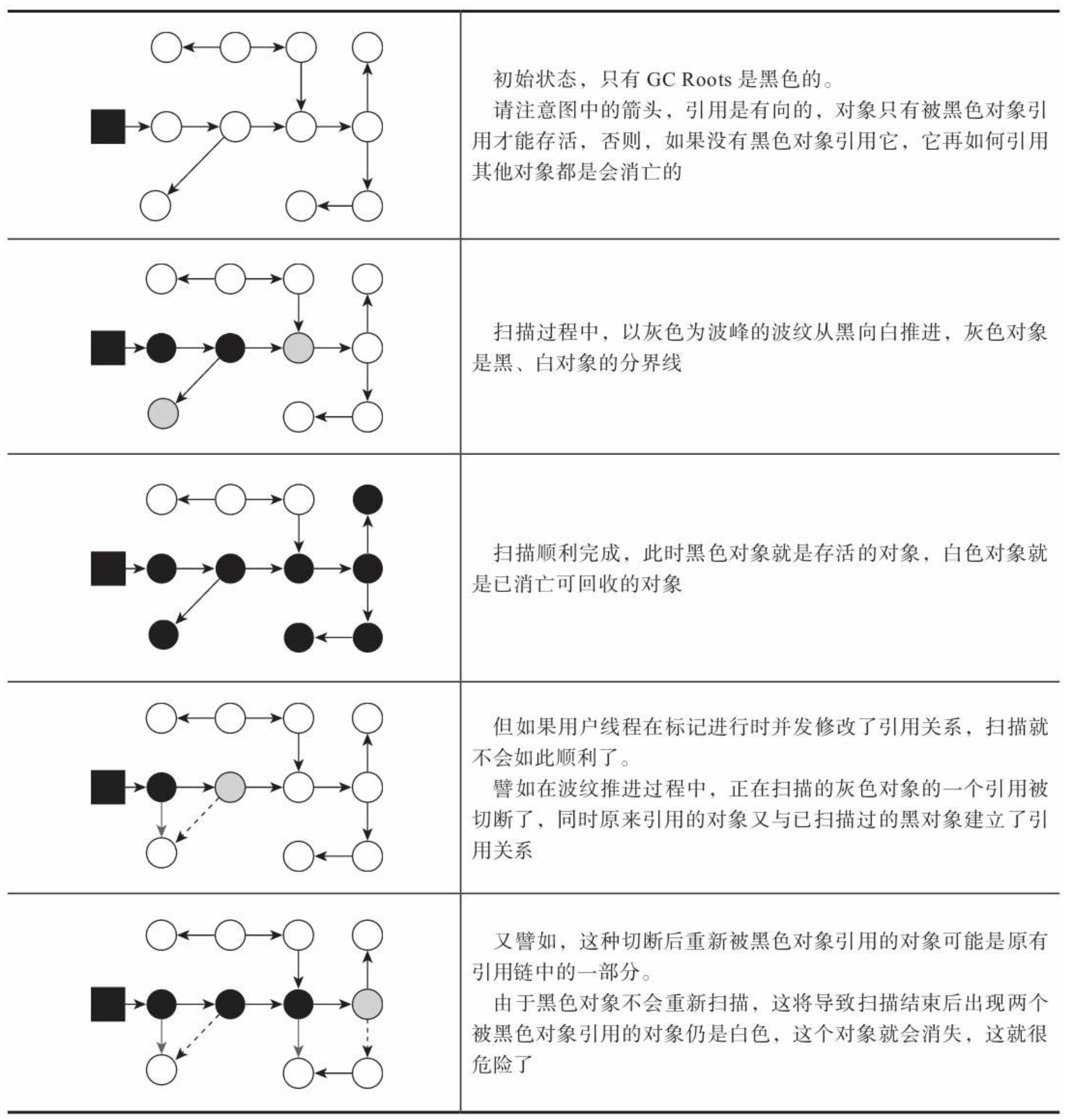
为解决该问题，需要破坏这两种情况的任意一个，由此分别产生了两种解决方案：

• 增量更新（Incremental Update）：当情况 1 发生时，记录新插入的引用；等待并发扫描结束后，以这些引用关系中的黑色对象为根重新扫描一次，即将这些新插入引用关系的黑色对象视作灰色对象处理

• 原始快照（Snapshot At The Beginning，SATB）：当情况 2 发生时，记录要删除的引用；等待并发扫描结束后，以这些引用关系中的灰色对象为根重新扫描一次，即按照刚开始扫描（最原始）的对象图快照进行搜索

4 经典垃圾收集器

• 新生代垃圾收集器：Serial、ParNew、Parallel Scavenge、G1

• 老年代垃圾收集器：Serial Old、Parallel Old、CMS、G1

* 注：JDK 9 中已完全取消对 Serial+CMS、ParNew+Serial Old 的支持

4.1 Serial 收集器

def 单线程的串行收集器

• 优点：

  • 简单高效：无线程交互的开销，单线程收集效率最高
  • 适用内存资源受限环境：在所有收集器中，消耗最少的额外内存（Memory Footprint），这是指为保证垃圾收集能够顺利高效地进行而存储的额外信息

• 缺点：垃圾收集时，必须由虚拟机在后台自动发起并暂停其他所有工作线程，直到收集结束。这个过程对用户而言是不可知、不可控的

• 应用：

  • HotSpot 虚拟机运行在客户端模式下的默认新生代收集器
  • 用户桌面应用、部分微服务应用：此类环境下，虚拟机管理的内存通常较小（i.e. 20M~200M），垃圾收集的停顿时间一般是可接受的（i.e. 10ms~50ms）

4.2 ParNew 收集器

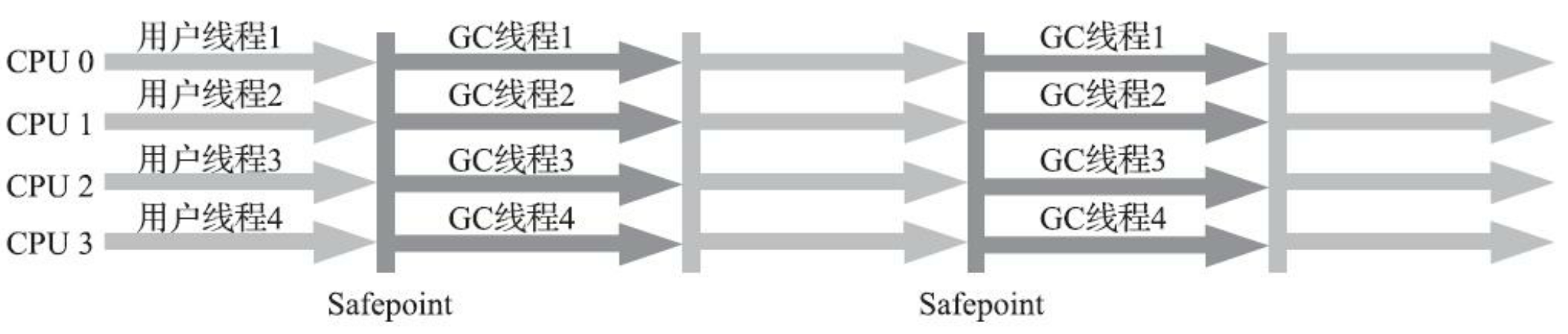
def Serial 收集器的多线程并行版本

• 优点：适用多核处理器环境，其默认开启的收集线程数等同于处理器的核心数量

• 缺点：存在线程交互的开销，在单核心处理器的环境表现不佳，即便在开启超线程后也无法保证对 Serial 收集器的优势

• 应用：激活 CMS 后的默认新生代收集器，且只有 ParNew 收集器能与 CMS 收集器配合工作，通过 -XX:+UseConcMarkSweepGC 选项开启

4.3 Parallel Scavenge 收集器

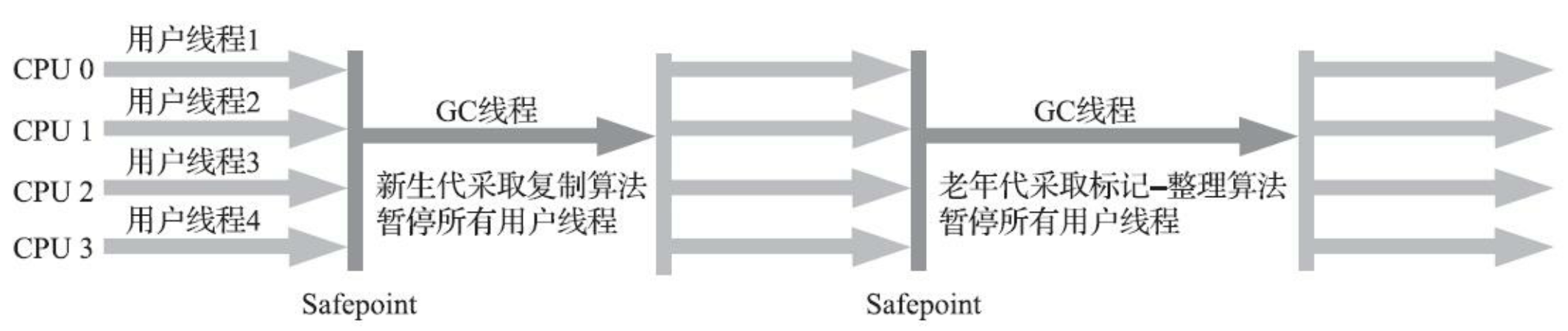
def 吞吐量优先收集器，类似 ParNew 收集器，但其主要目的是为了达到一个可控制的吞吐量（Throughput），即处理器用于运行用户代码的时间与处理器总消耗时间的比值越高越好，有

$$throughput=\frac{t_{user}}{t_{user}+t_{gc}}$$

• 优点：垃圾收集的自适应调节策略（GC Ergonomics）：开启 XX:+UseAdaptiveSizePolicy 选项，即无需人工指定新生代的大小（-Xmn）、Eden 与 Survivor 区的比例（-XX:SurvivorRatio）、晋升老年代对象大小（-XX:PretenureSizeThreshold）等细节参数。虚拟机会根据当前系统的运行情况收集性能监控信息，动态调整这些参数以提供最合适的停顿时间或者最大的吞吐量

* 注：Parallel Scavenge 收集器架构中本身有 PS MarkSweep 收集器进行老年代收集，但其实现与 Serial Old 几乎完全相同，故资料中常以 Serial Old 直接代替 PS MarkSweep

4.4 Serial Old 收集器

def Serial 收集器的老年代版本

• 应用：

  • HotSpot 虚拟机运行在客户端模式下的老年代收集器
  • （JDK 5 及之前）在服务端模式下，搭配 Parallel Scavenge 收集器使用
  • 在服务端模式下，作为 CMS 收集器发生发生 Concurrent Mode Failure 时的后备预案

4.5 Parallel Old 收集器

def Parallel Scavenge 收集器的老年代版本，JDK 6 开始提供

• 优点：适用注重吞吐量、处理器资源稀缺的环境

4.6 Concurrent Mark Sweep（CMS）收集器

def 并发低停顿收集器（Concurrent Low Pause Collector），其主要目的是为了获取最短的回收停顿时间，JDK 5 开始提供，JDK 9 起不推荐使用（Deprecate)。运作过程分为四个步骤：

Step 1：初始标记（CMS initial mark），标记 GC Roots 能直接关联的对象，需要停顿用户线程

Step 2：并发标记（CMS concurrent mark），进行可达性分析，从 GC Roots 的直接关联对象开始遍历整个堆中的对象图，但无需停顿用户线程，即收集器线程可同用户线程一起工作

Step 3：重新标记（CMS remark），修正 Step 2 中因用户程序继续运作而导致标记产生变动的那一部分对象的标记记录，需要停顿用户线程

Step 4：并发清除（CMS concurrent sweep），清理标记对象，无需停顿用户线程

各阶段的执行速度对比：$1 ＞ 3 ＞ 4 \gg 2$

• 优点：并发收集、低停顿

• 缺点：

  • 吞吐量较低：CMS 不会导致用户线程停顿，但因占用部分线程导致应用程序变慢，从而降低总吞吐量，i.e. 当处理器核心数量不足四个时，CMS 对用户程序的影响就可能变得很大，高处理器负载时甚至可能导致用户程序的执行速度忽然大幅降低
  • 无法处理 “浮动垃圾”（Floating Garbage）：可能出现 Concurrent Mode Failure，进而导致另一次 “Stop The World” 的 Full GC。浮动垃圾是指在并发标记和并发清理阶段，用户线程继续运行产生的新的垃圾对象。由于这些对象出现在标记过程结束以后，CMS 无法在当次收集中处理，只能保留至下一次垃圾收集时再做清理
  • 内存空间碎片问题

4.7 Garbage First（G1）收集器

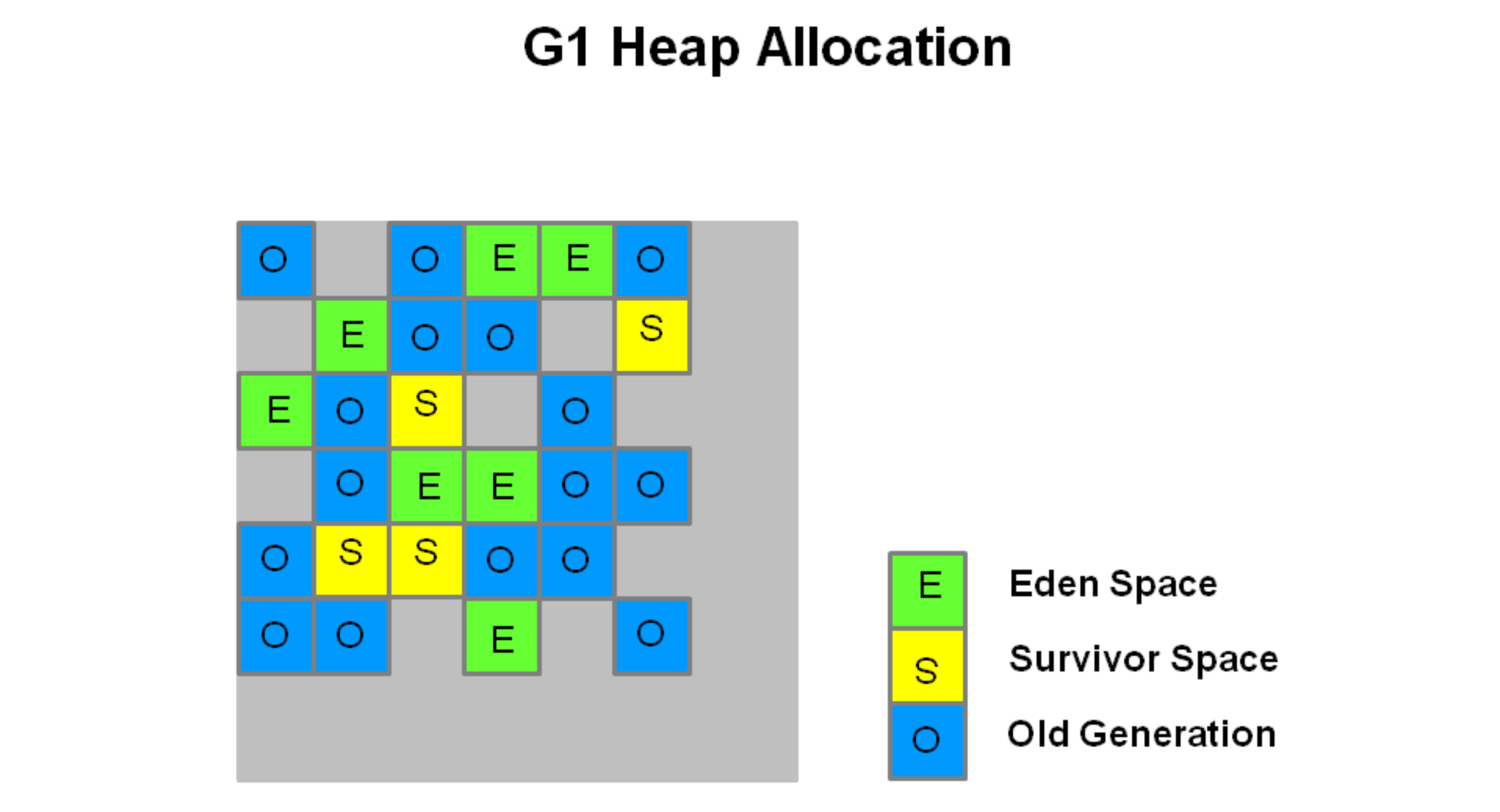
def 全功能的垃圾收集器（Fully-Featured Garbage Collector），其主要目的是为了建立起 “停顿时间模型”（Pause Prediction Model）的收集器，即能够支持指定在一个长度为 M 毫秒的时间片段内，消耗在垃圾收集上的时间大概率不超过 N 毫秒。因此，G1 收集器开创了基于 Region 的堆内存布局，不再隔离新生代和老年代，把连续的 Java 堆划分为多个大小相等的独立区域（Region)，每一个 Region 都可以根据需要，扮演新生代的 Eden 空间、Survivor 空间，或者老年代空间。JDK 8 Update 40 后正式提供，用于替代 CMS

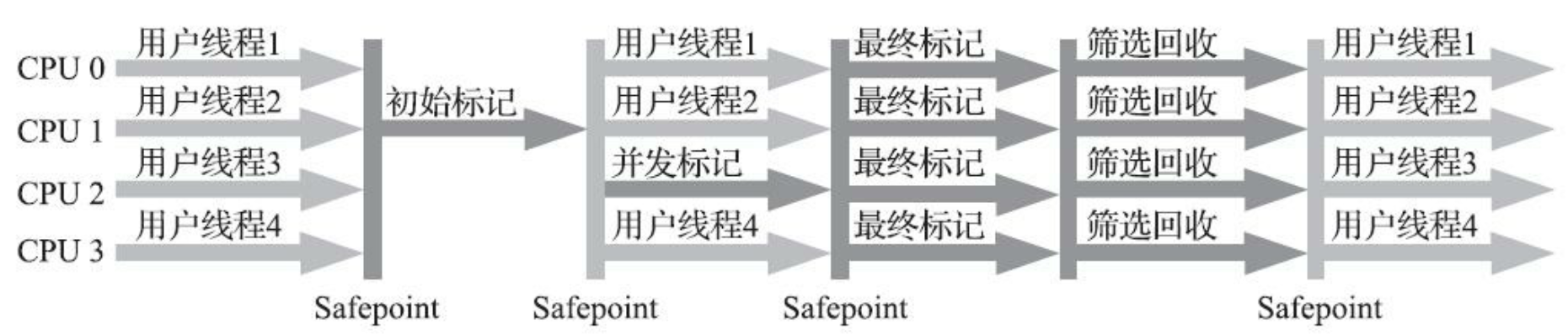
在不考虑用户线程运行过程中的动作时（如收集器对记忆集的维护等），G1 收集器的运作过程分为四个步骤：

Step 1：初始标记（Initial Marking），标记 GC Roots 能直接关联到的对象，修改 TAMS 指针的值，需要停顿用户线程

Step 2：并发标记（Concurrent Marking），进行可达性分析，从 GC Roots 的直接关联对象开始遍历整个堆中的对象图，无需停顿用户线程

Step 3：最终标记（Final Marking），再次短暂暂停用户线程，处理遗留的少量 SATB 记录，即修正 Step 2 中因用户程序继续运作而导致标记产生变动的那一部分对象的标记记录

Step 4：筛选回收（Live Data Counting and Evacuation），更新 Region 的统计数据，将各个 Region 的回收价值和成本排序，再自由选择任意个 Region 构成回收集，把回收集中 Region 包含的的存活对象复制到空的 Region 中，最后清理旧 Region 的全部空间。需要停顿用户线程

* 注：虽然 G1 整体上基于 “标记 - 整理” 算法实现，但从 Step 4 可知，局部（两个 Region 之间）上是基于 “标记 - 复制” 算法实现的

• 优点

  • 并发收集、可预测的低停顿：可由用户指定 -XX：MaxGCPauseMillis 参数以设置期望的停顿时间（默认为 200ms），从而动态地在吞吐量和延迟之间寻求平衡
  • 收集效率高，现在新生代和老年代是一系列（无需连续的）Region 的动态集合，每次收集到的内存空间都是 Region 大小的整数倍，从而有计划地避免在整个 Java 堆中进行全区域的垃圾收集
  • 可按收益动态确定回收集
  • 不会产生空间碎片

• 缺点：

  • 更高的内存占用（Footprint）负担：相较于其他经典收集器，一般至少需要耗费大约相当于 Java 堆容量 10%~20% 的额外内存来维持 G1 收集器的工作
  • 相较于 CMS 收集器，程序运行时带来更高的额外执行负载（Overload）

• 应用：HotSpot 虚拟机运行在服务端模式下的默认垃圾收集器

参考

[1] 深入理解 Java 虚拟机：JVM 高级特性与最佳实践（第 3 版）

[2] Java JVM 虚拟机 已完结（IDEA 2021 版本）4K 蓝光画质

[3] 柏码知识库 | JVM 笔记（二）内存管理

[4] Java 全栈知识体系

[5] JVM 垃圾回收（GC）机制（一文读懂）

[6] Garbage First Garbage Collector Tuning

[7] Getting Started with the G1 Garbage Collector

[8] 《深入理解 Java 虚拟机》（三）垃圾收集器与内存分配策略

[9] Hosking A L, Hudson R L. Remembered sets can also play cards[J]. OOPSLAGC OOP93]. Available for anonymous FTP from cs. utexas. edu in/pub/garbage/GC93, 1993.

4 安全规约基础

4.1 预备知识

4.1.1 计算问题 Computing Problem

def 用数学原语（mathematical primitive）定义的计算问题表示特定问题和答案的数学对象，其具有无限数目的实例 - 解决方案对 $(x, y)$

• 使用算法（algorithms）解决计算问题

• 查找 $y$ 的计算开销随着 $x$ 长度的增加而增加

• 计算问题 = 计算性问题 + 判定性问题

4.1.2 计算 / 搜索性问题 Computational Problem

def 在计算性问题中，问题实例 $x$ 的解决方案 $y$ 来自一个大的解空间，譬如$2^{|x|}$
e.g. CDHP：实例 $x =(g, g^a,g^b) ∈G$; 解决方案 $y=g^{ab} ∈G$

4.1.3 判定性问题 Decisional Problem

def 在判定性问题中， 问题实例 x 的解 y 来自集合 {0, 1}，只有两个答案：

• 如果 y = 1，则实例 x 称为 true 实例

• 如果 y = 0，则实例 x 称为 false 实例
  e.g. DDHP

1. 正直语言 Formal Language

def 包含所有 true 实例的集合称为正直语言 $L$，判定性问题转化为判断 $x∈ L$ 是否成立

4.1.4 决定性算法 Deterministic Algorithms

def 给定一个问题实例 x 作为输入，始终返回解决方案 y 作为正确的结果

4.1.5 概率性算法 Probabilistic Algorithms

def 给定一个问题实例 x 作为输入，有一定可能给出正确的结果

• 比决定性算法更高效

• $(t, ϵ)$：

  • $t$：时间差，要求为概率多项式时间 PPT
  • $ϵ$：概率 / 优势

1. 为什么要求为概率多项式时间 PPT？

若为指数时间，则攻破了方案还未攻破困难问题，即方案的安全性较困难问题弱了很多

2. $\epsilon$ 什么时候是优势，什么时候是概率？

• 对计算性问题，$ϵ$ 是成功概率（success probability）

• 对判定性问题，$ϵ$ 是解决问题的优势（advantage）

4.1.6 算法的分类

所有对象（构造方案、中断方案、解决问题和程序规约）都是为了提出算法。在密码学中，算法可以分为：

• 方案算法：用于构建密码系统（方案）

• 攻击算法：用于打破一个方案

• 求解算法：用于解决一个困难问题

• 规约算法：用于描述安全规约

4.1.7 多项式与指数

def 令 f (λ) 是关于正数 λ 的函数，有：

• 多项式（Polynomial）：存在 $c, k > 0$ 使得 $f (λ) ≤ c·λ^k$

  • 多项式时间：理解为多项式速度，$f(λ)$ 增加的速度取决于 $λ$ 的长度

• 指数（Exponential）：存在 $c > 0$ 使得 $2^{c·λ}≤f (λ)$ （变量在方幂上）
  e.g. $2^{160}$ 不是指数时间，$2^λ$ 是指数时间

4.1.8 不可忽略 Non-Negligible/Noticeable

def $1−negl(λ)$ ：如果对于任何整数 $k_1∈Z$，存在另一个整数 $k_2∈Z$，对 $λ> k_2$ ，函数 $negl(λ)<1/λ^{k_1}$，则函数 $1−negl(λ)$ 在 $λ$ 中是不可忽略的

4.2 困难问题

4.2.1 计算性困难问题

def 假设由安全参数 λ 生成一个计算性问题，给定一个问题实例并将其作为输入，在多项式时间内找到该问题实例正确解的概率是 λ 的可忽略函数 $ϵ(λ)$

$$Pr⁡[A(x) = y] ≤ ϵ(λ)$$

• 对手 $A$ 运行概率算法

• 对手在多项式时间内中止

• $ϵ(λ)$ 是 $λ$ 中的可忽略函数

• 问题实例 $x$ 的长度为 $λ$

4.2.2 判定性困难问题

def 假设由安全参数 λ 生成一个判定性问题，给定一个目标为 Z 的问题实例作为输入，在多项式时间内输出正确猜测的优势是 λ 的可忽略函数 $ϵ(λ)$

$$|Pr⁡[A(x)=True│x=true]-Pr⁡[[A(x)=True│x=false]|≤ϵ(λ)$$

• 对手 $A$ 运行概率算法

• 对手在多项式时间内中止

• $ϵ(λ)$ 是 $λ$ 中的可忽略函数

• 问题实例 $x$ 的长度为 $λ$

1. 困难问题和困难问题假设的区别？

打破方案意味着解决困难难题，因此方案在此困难问题假设下是安全的

4.2.3 强假设与弱假设

• 弱假设

  • def 又称标准假设，其安全级别仅与生成底层数学原语所输入的安全参数有关
  • 安全级别非常接近 DLP，攻破的时间成本高
  • 当且仅当几个条件成立时，计算问题才很难

• 强假设

  • def 其安全级别不仅与生成底层数学原语所输入的安全参数有关，还与其他参数有关，譬如每个问题实例的大小
  • 安全级别低于 DLP，攻破的时间成本低于弱假设
  • 当且仅当许多条件成立时，计算问题才很难

1. 什么样的方案安全性更好？

4.2.4 计算性困难问题实例

设 $G$ 和 $G_τ$ 是 $e:G×G→G_τ$ 且 $G=<g>$ 的循环群

4.2.5 判定性困难问题实例

4.3 安全级别

从攻击算法的角度，为达到 k-bit 安全性，有：

$$2^k=min\{t_1/ϵ_1 ,t_2/ϵ_2 ,⋯,t_l/ϵ_l \}$$

• 已知（known）安全级别：基于所有已知的攻击算法

• 确切（exact）安全级别：基于最佳攻击算法，通常是未知的，否则证明$NP ≠ P$ 是容易的

• 安全级别上限（upper bound）：基于比破坏方案更难的 DP

• 安全级别下限（lower bound）：基于安全规约采用的困难问题假设

4.4 一次一密 One-Time Pad

def 令 $E(m,r,R)$ 是由公共参数 $R$ 和秘密参数 $r$ 对给定消息 $m$ 的加密。如果对于来自同一明文空间的任意两个不同消息 $m_0$, $m_1$，在公共参数 $R$ 下，$CT$ 可以等概率地表示为由秘密参数 $r_0$ 对消息 $m_0$ 的加密，或者由秘密参数 $r_1$ 对消息 $m_1$ 的加密，即 $Pr[CT=E(m_0,r_0,R)]=Pr[CT=E(m_1,r_1,R)]$，那么密文 $E(m,r,R)$ 是一次一密

参考资料：

[1] 安全规约导论，郭富春

3 基于群的密码学基础

3.1 有限域 Finite Field

3.1.1 有限域的定义

def 有限域（伽罗瓦域）用 $(F, +, ∗)$ 表示，是一个包含有限数量元素的集合，其两个二进制运算加法 $+$ 和乘法 $∗$ 定义如下：

• ① 封闭性：对$∀u, v ∈ F$，有 $u + v ∈ F$ 且 $u ∗ v ∈ F$

• ② （加法）结合律：对 $∀u_1, u_2, u_3 ∈ F$，有$(u_1 + u_2) + u_3 = u_1 + (u_2 + u_3)$ 且 $(u_1 ∗ u_2) ∗ u_3 = u_1 ∗ (u_2 ∗ u_3)$

• ③ 交换律：对 $∀u, v ∈ F$，有 $u + v = v + u$ 且 $u ∗ v = v ∗ u$

• ④ 单位元：对 $∃0_F, 1_F ∈ F$ 和 $∀u ∈ F$，有 $u + 0_F = u$ 且 $u ∗ 1_F = u$

• ⑤ 负元：对 $∀u ∈ F$，$∃–u ∈ F$ 使得 $u + (–u) = 0_F$

• ⑥ 去零元：对 $∀u ∈ F^∗$, $∃u^{−1} ∈ F^∗$ 使得 $u ∗ u^{−1} = 1_F$，其中 $F^∗ = F/{0_F}$

• ⑦ 分配律：对 $∀u_1, u_2, v ∈ F$，有 $(u_1 + u_2) ∗ v = u_1 ∗ v + u_2 ∗ v$

3.1.2 域运算

可扩展至减法和除法：

• 减法：由⑤有 $u − v = u + (−v)$，其中 $-v$ 是 $v$ 的加法逆元

• 除法：由⑥有 $u/v = u ∗ v^{−1}$，其中 $v^{−1}$ 的乘法逆元

3.1.3 域的选取

一般选取一组大素数以防止爆破攻击，因此 $p(x)=p_0+p_1 x+p_2 x^2+⋯+p_{n-1} x^{n-1}∈F_p (x)$ 是不可约（irreducible）的，其系数仍在 $F_p$ 级别。可约的情况譬如：$x^2 - 2$

• 基础域：用 $(F_p, +, ∗)$ 表示

• 扩域（extended field）：用 $(F_{p^n}, +, ∗)$ 表示

3.2 循环群 Cyclic Groups

3.2.1 群的定义

• 阿贝尔群：用 $(H, ·)$ 表示，是一组具有二元运算 $·$ 的元素，满足①~⑤

• 循环的阿贝尔群：在满足①~⑤的前提下，群内任意元素均可由生成元 $h$ （群的方幂）生成，即：$H={h^0,h^1,h^2, ⋯,h^{|H|-1}}$，其中群 $H$ 的阶 $|H|$ 满足 $h^{|H|}=h^0=1_H$

• 素数阶的循环阿贝尔群：如果群 $G$ 是循环群 $H$ 的子群且 $|G|$ 为素数，则$G$ 是素数阶的循环子群，其中是 $|G|$ 是 $|H|$ 的除数，存在生成元 $g ∈ H$ 生成群 $G$

3.2.2 素数阶的循环群

1. 使用循环群和素数阶的原因？

• $G$ 是没有禁闭攻击（confinement attack）的最小子群。禁闭攻击是指攻击者试图将计算限制在一个特定的子群中，从而破坏整个方案的安全性；同时，若 $G$ 包含了不必要元素，可能带来不必要的复杂性和开销

  • 目前，$p=2^{160}$ 的 160bit 长度以上比较安全，因破解离散对数问题需要 $O(p^{1/2})$，达 80bit 安全

• 除 $g^0$ 之外的任何元素都是 $G$ 的生成元

• $\{1, 2, · · · , p-1\}$ 中的任意整数都具有模乘逆元

• 对任意 $x∈Z_p^∗=\{1,2,⋯,p-1\}$，均能计算 $g^{1/x}=g^{x^{-1}}$

2. 若要为密码学方案构造一个群，需要指定哪些参数？

$(G, g, p)$：

• $G$：群的空间，是一个包含元素的集合，这些元素作为群成员

• $g$：群的生成元

• $p$：群的阶

3. 每个组元素的表示大小是多少？

对素数 $p$，有 $G = \{g^0,g^1, · · · ,g^{p-1}\}$

• 群中有 $p$ 个元素，每个元素具有相同的大小

• 群中的每个元素都可以编码为二进制字符串

• 群中的每个元素必须用不同的二进制字符串表示

3.2.3 群幂 Group Exponentiations

设 $(G, g, p)$ 为循环群，$x∈Z_p$，用 $g^x$ 表示群幂：

• 群幂由上述定义中的群运算的 $x−1$ 个副本（copies）组成

• 当 $x$ 大于 $2^{160}$ 时，执行 $x−1$ 个副本的计算是不切实际的

• 存在快速计算群幂的算法：平方乘法（square-and-multiply）算法

3.2.4 离散对数问题 Discrete Logarithms Problem

群中最基本的难题是离散对数问题，给定 $g, h∈G/{1_G}$，有：

• 满足 $g^x= h$ 的整数 $x$ 称为离散对数

• 计算 $x$ 称为离散对数问题

1. 群使用素数阶的另一原因？

如果 $G$ 是素数阶的群，则对于任意两个群元素 $g, h∈G/{1_G}$，离散对数 $x$ 必须存在

2. 破解离散对数问题的时间复杂度？

设 $(G, g, p)$ 为任意群，求解 DLP 的最有效算法需要 $O(p^{1/2})$

3. 若要为密码学方案构造一个群，需要考虑哪些攻击？

• 泛型攻击（generic attacks）：参数必须满足 $p ≥ 2^{160}$

• 特定攻击（specific attacks）：为特定群构造的所有其他参数必须足够大，譬如群元素大小

3.2.5 来自有限域的循环群

有限域 $(F_{p^n},+,∗)$ 已包含的两类群：$(F_{p^n},+)$ 和 $(F_{p^n}^∗,∗)$；此外引入椭圆曲线 ECC 上的群

1. 为什么要使用椭圆曲线上的群？

• 同等安全性下，ECC 短于基于域的元素长度，存储开销低适用受限设备

  • 原因：只需要存储 x 坐标 + 0/1（上方 / 下方）的一个比特

3.2.6 群的选取

• 乘法群 $(G, g,p,q)$

  • 群的元素：从 $Z_p^∗=\{1,2,⋯,p-1\}, |g| =log_2 p$ 中选取的整数
  • 群的生成元：$g$ 从 $Z_p^∗$ 中选取，注意不是 $Z_p^∗$ 中所有的整数都是生成元
  • 群的阶：$q|(p − 1)$，$q$ 和 $p-1$ 同余
  • 群的运算：$u · v = u × v mod p$
  • 安全性：为达到 80bit 安全，$q$ 应至少为 1024 bits

• 椭圆曲线上的群 $(G, g, p)$：椭圆曲线是一条定义在 $F_{p^n}$ 上的光滑曲线，所有的点都在 $y^2=x^3+ax+b$ 上，其中 $a,b∈F_{p^n}$

  • 群的元素：椭圆曲线上的点集，每个点用 x 坐标和 y 坐标表示
  • 群的生成元：$g$ 亦为一个点
  • 群的阶： $p$ 是素数阶
  • 群的运算：对 $u,v∈G$ 和 $x∈F_p$，计算 $u+v$ 或 $x·u$
  • 安全性：群元素大小可以与群的阶一样短，为达到 80bit 安全，$|g|= |p|= 160$，$q$ 应至少为 160 bits

3.2.7 群上的计算

• 群的运算：给定 $g, h∈G$，计算 $g·h$

• 群上求逆元：给定 $g∈G$，计算  $1/g=g^{-1}$

  • 由 $g^p=g·g^{p-1}=1_G$, 有 $g^{-1}=g^{p-1}$

• 群上的除法：给定 $g, h∈G$，计算 $h/g=h·g^{-1}$

• 群上的幂运算：给定 $g∈G$ 和 $x∈Z_p$，计算 $g^x$

3.3 双线性配对 Bilinear Pairings

双线性配对的三种类型：

• I 型：$G_1=G_2$（对称）

• II 型：$G_1≠G_2$，且能找到同态 $ψ ：G_2→G_1$

• III 型：$G_1≠G_2$，但没有有效的同态

3.3.1 对称配对 $e:G×G→G_T$

两类 DLP：

• 从 $g$ 和 $g^x$ 计算 $x$

• 从 $e(g,g)$ 和 $e(g,g)^x$ 计算 $x$
  为保证 80bit 安全，需要 $|g| ≥ 512, |e(g, g)| ≥ 1024$

3.3.2 非对称配对 $e:G_1×G_2→G_T$

三类 DLP：

• 从 $g_1$ 和 $g_1^x$ 计算 $x$

• 从 $g_2$ 和 $g_2^x$ 计算 $x$

• 从 $e(g_1,g_2)$ 和 $e(g_1，g_2)^x$ 计算 $x$
  为保证 80bit 安全，需要 $|g_1 | ≥ 160, |g_2 | ≥ 1024, |e(g_1,g_2)| ≥ 1024$
  构造非对称配对时，还需注意以下问题：

• 由于非对称结构，需设置 $|g_2 | = |e(g_1,g_2))|$

• 椭圆曲线由基于配对的密码学 （PBC） 库中的 Curve-F 专门定义，其中 $y^2=x^3+b$ 和 $k=12$

3.3.3 双线性配对群上的计算

双线性配对群由素数阶 $p$ 的群 $(G,G_T)$ 或 $(G_1,G_2,G_T)$ 和双线性映射 $e$ 组成，其计算包括：

• 所有在域 $Z_p$ 上的模（幂）运算

• 对群 $(G,G_T)$ 或 $(G_1,G_2,G_T)$ 上的所有运算

• $∀ u, v ∈ G$ 的双线性配对 $e(u, v)$

3.4 哈希函数 Hash Functions

哈希函数将任意长度的字符串作为输入，并返回一个更短的字符串作为输出

3.4.1 哈希函数的分类

1. 根据安全定义分类

• 单向（One-Way）哈希函数：给定一个单向哈希函数 $H$ 和一个输出字符串 $y$，很难找到满足 $y=H(x)$ 的输入 $x$

• 抗碰撞（Collision-Resistant）哈希函数：给定一个抗碰撞哈希函数 $H$，很难找到两个不同的输入 $x_1$ 和 $x_2$ 满足 $H(x_1 )=H(x_2)$

2. 根据输出空间分类

• $H: \{0, 1\}^∗→\{0, 1\}^n$：输出空间是包含所有 n 位字符串的集合

  • 主要用于从密钥空间 $\{0, 1\}^n$ 生成一个对称密钥，用于混合加密

• $H: \{0, 1\}^∗→Z_p$：输出空间为 $\{0, 1, 2, · · · , p-1\}$，其中 $p$ 是群的阶

  • 主要用于将哈希值嵌入到群的指数，譬如 $g^{H(m)}$

• $H : \{0, 1\}^∗ → G$：输出空间是一个循环群，即将输入字符串哈希映射到一个群元素

  • 仅适用于某些群，主要是对称双线性配对 $G×G→G_T$ 中的群 $G$ 和非对称双线性配对 $G_1×G_2→G_T$ 中的群 $G_1$

3.5 伪随机数生成器 (Pseudo) Random Number Generator

设 $x$ 为随机变量，$w1$、$w2$ 为空间中任意两个可能的随机数，进行随机选择操作，使得 $Pr⁡[x=w_1 ]=Pr⁡[x=w_2]$

1. 方案中的随机数和现实中的区别？

• 在方案算法中，算法可以选择满足相等概率的真正随机的随机数

• 在现实世界中，算法是使用伪随机数生成器选择伪随机数

参考资料：

[1] 安全规约导论，郭富春

1 引入

1.1 柯克霍夫原则 Kerckhoffs’s Principle

• def 即使密码系统的任何细节已为人悉知，只要密钥或未泄漏，它也应是安全的

• 加密系统的安全性不应依赖于算法的保密性，而应基于加密密钥的保密性

1.2 公钥密码学 Public-key Cryptography

• def

  • 每个用户都有一对密钥：私钥和公钥
  • 公钥是公开已知的，但私钥是保密的
  • 给定公钥，推断出私钥在计算上是不可行的

• 分类

  • 公钥加密：允许双方通过不安全的通道交换消息，提供了保密性
  • 数字签名：允许双方对电子文档进行签名，提供了不可伪造性

1.3 安全

• 过去的验证方式：搜索攻击（search for attacks），存在问题：

  • 永远无法确定攻击不存在
  • 安全性最多只能被视为启发式的，不能排除存在未知攻击方式的可能性

1.3.1 可证明安全

• def 旨在将方案的安全性与困难问题联系起来，先指定攻击者能力和方案的安全目标，再将破坏方案安全目标的敌手转变为针对该方案所基于的困难问题的安全目标的敌手。

• 分类

  • 基于游戏的证明 Game-based Proof
    • 安全规约：若存在敌手 $A$ 能破坏方案，则存在有效算法 $B$ 借助 $A$ 解决困难问题。
    • Game Hopping：在特定攻击环境中运行的攻击者具有未知的成功概率，改变攻击环境直到可以计算出攻击者的成功概率
  • 基于模拟的证明 Simulation-based Proof

1.3.2 渐近安全与具体安全

• 渐近安全：使用多项式时间可归约性对计算问题的难度进行分类

• 具体安全：实际上由于需要实例化安全参数，需确切知道减少的效率，参数化敌手可用的所有资源

• def 若对手可以在时间 $t$ 中以至少 $ε_Σ$ 的概率打破方案 $Σ$，则存在敌手可以在时间 $t'$ 内以至少 $ε_Π$ 的概率打破困难问题 $Π$，其中 $t≈t^′$， $ε_Σ ≈ε_Π$

• 安全参数 $λ$ 的选取：$ε_Π=2^{-λ}-γ$

2 概念、定义和模型

2.1 常用符号及定义

2.2 数字签名

2.2.1 数字签名的算法定义

• $Setup(1^λ )→params$

• $KeyGen(1^λ,params)→(SK,PK)$

• $Sign(M,SK,params)→σ$

• $Verify(M,σ,PK,params)→0/1$

2.2.2 数字签名的安全模型

def 安全模型：定义敌手所知道的内容，不同安全模型破坏方案的难度不同

1. 针对选择消息攻击的存在不可伪造性 EU-CMA

游戏在挑战者 $C$ 和敌手 $A$ 之间的执行过程：

• $Setup$：$C$ 运行 $Setup(1^λ )→params$，并将 $params$ 返回给 $A$

• $KeyGen$：$C$ 运行 $KeyGen(1^λ，params)→(SK，PK)$，并将 $PK$ 返回给 $A$

• $Query$：

  • 动态地提交消息 $M_i$
  • $C$ 运行 $Sign(M_i，SK，params)→σ_i$，并将 $σ_i$ 返回给 $A$
    • 其中 $i=\{1,2，⋯, q_S\}$
    • 设消息 $M=\{M_1, ⋯, M_{q_S }\}$
    • 设$Q=\{(M_1, σ_1 ), ⋯, (M_{q_s}, σ_{q_s } )\}$

• $Forgery$：$A$ 在消息 $M^∗$ 上输出签名 $σ^∗$。满足下述情况则 $A$ 将赢得游戏：

  • $Verify(M^∗, σ^∗, PK, params)→1$
  • $M^∗∉M$

2. 针对选择消息攻击的强不可伪造性 SU-CMA

游戏在挑战者 $C$ 和敌手 $A$ 之间的执行过程：

• $Setup$：$C$ 运行 $Setup(1^λ )→params$，并将 $params$ 返回给 $A$

• $KeyGen$：$C$ 运行 $KeyGen(1^λ，params)→(SK，PK)$，并将 $PK$ 返回给 $A$

• $Query$：

  • 动态地提交消息 $M_i$
  • $C$ 运行 $Sign(M_i，SK，params)→σ_i$，并将 $σ_i$ 返回给 $A$
    • 其中 $i=\{1,2，⋯, q_S\}$
    • 设消息 $M=\{M_1, ⋯, M_{q_S }\}$
    • 设$Q=\{(M_1, σ_1 ), ⋯, (M_{q_s}, σ_{q_s } )\}$

• $Forgery$：$A$ 在消息 $M^∗$ 上输出签名 $σ^∗$。满足下述情况则 $A$ 将赢得游戏：

  • $Verify(M^∗, σ^∗, PK, params)→1$
  • $(M^∗, σ^∗)∉Q$：$A$ 可以询问关于 $M^∗$ 的签名，但输出一个不同的签名即可

2.3 公钥加密

2.3.1 公钥加密的算法定义

• $Setup(1^λ )→params$

• $KeyGen(1^λ,params)→(SK,PK)$

• $Enc(M,PK,params)→CT$

• $Dec(CT,SK,params)→M/⊥$

2.3.2 公钥加密的安全模型

1. 针对选择明文攻击的不可区分性 IND-CPA

游戏在挑战者 $C$ 和敌手 $A$ 之间的执行过程：

• $Setup$：$C$ 运行 $Setup(1^λ )→params$，并将 $params$ 返回给 $A$

• $KeyGen$：$C$ 运行 $KeyGen(1^λ，params)→(SK，PK)$，并将 $PK$ 返回给 $A$

• $Challenge$：

  • $A$ 提交两条消息 $M_0$ 和 $M_1$
  • $C$ 掷出一枚无偏硬币，得到比特 $b∈ \{0,1\}$
  • $C$ 运行 $Enc(M_b, PK, params)→CT^∗$，并返回 $CT^∗$ 给 $A$

• $Output$：$A$ 在 $b$ 上输出其猜测 $b'$，如果 $b^′=b$ ，则 $A$ 赢得游戏

2. 针对（两阶段）选择密文攻击的不可区分性 IND-CCA2

游戏在挑战者 $C$ 和敌手 $A$ 之间的执行过程：

• $Setup$：$C$ 运行 $Setup(1^λ )→params$，并将 $params$ 返回给 $A$

• $KeyGen$：$C$ 运行 $KeyGen(1^λ，params)→(SK，PK)$，并将 $PK$ 返回给 $A$

• $Phase$ I：

  • $A$ 动态地提交密文 $CT_i$，其中 $i=1, 2, ⋯, q_1$
  • $C$ 运行 $Dec(CT_i,SK,params)→M_i$，并将 $M_i$ 返回给 $A$

• $Challenge$：

  • $A$ 提交两条消息 $M_0$ 和 $M_1$
  • $C$ 掷出一枚无偏硬币，得到比特 $b∈ \{0,1\}$
  • $C$ 运行 $Enc(M_b, PK, params)→CT^∗$，并返回 $CT^∗$ 给 $A$

• $Phase$ II：

  • $A$ 动态地提交密文 $CT_j$，但有以下限制条件：
    • $CT^∗ ≠  CT_j$ ，其中 $j=1,2,⋯,q_2$
    • $C$ 运行 $Dec(CT_j,SK,params)→M_j$, 并将 $M_j$ 返回给 $A$
    • $q_D=q_1+q_2$

• $Output$：$A$ 在 $b$ 上输出其猜测 $b'$，如果 $b^′=b$ ，则 $A$ 赢得游戏