1 方案介绍
1.1 无证书签名方案 CLSS
-
Setup(k):系统初始化
-
PPKE(UIDi,s):部分密钥生成
-
SPRK(UIDi,di):设置用户完整私钥
-
SPK(UIDi,svi):设置用户公钥
-
Sign(Mi,ski,UIDi,pki):签名
-
Verify(Mi,σi,UIDi,pki):单次验证
-
BatchVerify({Mi,σi,UIDi,pki}i=1n):批量验证
1.1.1 系统初始化
Setup(k):由 KGC 执行,根据安全参数生成主密钥和参数列表
-
给定安全参数 k,生成参数集合 ⟨G1,G2,ψ,GT,e,q,P,P′⟩
-
随机选取 s∈Zq∗ 作为主私钥,计算主公钥 P0=sP,P0′=sP′
-
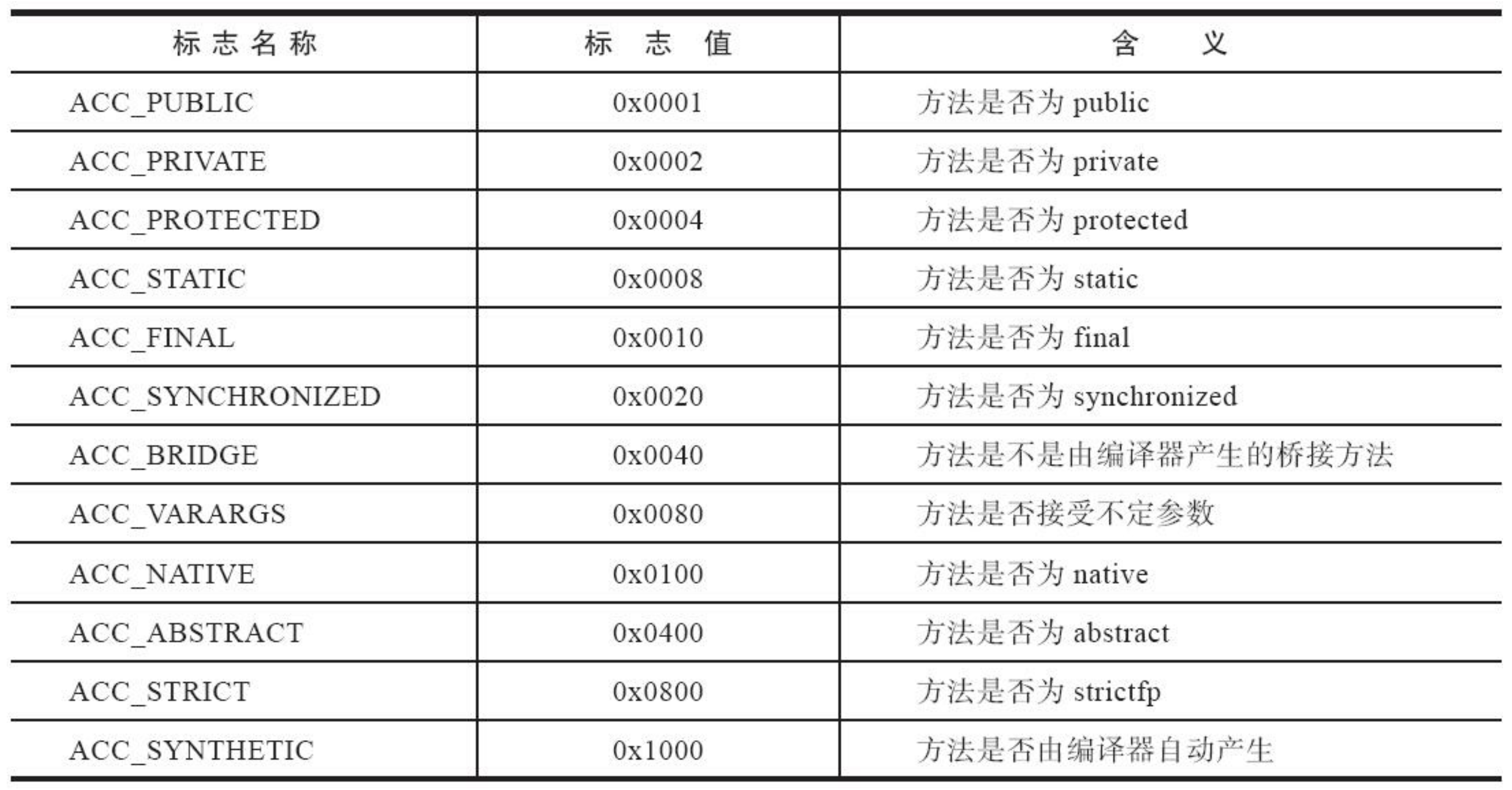
选择三个密码学哈希函数H0:{0,1}∗→G1∗, H1:{0,1}∗→Zq∗, H2:{0,1}∗→G2∗
-
公开参数列表 paramList={G1,G2,ψ,GT,e,q,P,P′,P0,P0′,H0,H1,H2}
1.1.2 部分密钥生成
PPKE(UIDi,s):由 KGC 执行,接受用户身份 UIDi∈{0,1}∗ 和主私钥 s 作为输入,生成用户部分私钥 di
1.1.3 设置完整私钥
SPRK(UIDi,di):由具有 UIDi 身份的用户执行,输入身份 UIDi 和部分私钥 di,生成其完整私钥 ski
-
选择随机数 svi∈Zq∗ 作为其秘密值
-
设置完整私钥 ski=(svi,di)
1.1.4 设置公钥
SPK(UIDi,svi):由具有 UIDi 身份的用户执行,输入用户身份 UIDi 和秘密值 svi,生成用户公钥 pki
1.1.5 签名
Sign(Mi,ski,UIDi,pki):由具有 UIDi 身份、完整私钥 ski 和公钥 pki 的签名者执行,输入消息 Mi、ski、UIDi 和 pki,生成对消息 Mi 的签名 σi
-
随机选取 ri∈Zq∗,设置 Ri=riP
-
计算 ui=H1(UIDi∣∣Mi∣∣pki∣∣Ri∣∣Δ) 和 W=H2(Δ),其中 Δ 是基于时间戳生成的一次性消息
-
计算 Vi=uisviψ(W)+uidi+ri(ψ(W)+P0)
-
设置签名 σi=(Ri,Vi)
1.1.6 验证
Verify(Mi,σi,UIDi,pki):输入消息 Mi、签名 σi、用户身份 UIDi 和用户公钥 pki,验证者验证签名 σi 的有效性
-
计算 Qi=H0(UIDi),ui=H1(UIDi∣∣Mi∣∣pki∣∣Ri∣∣Δ),W=H2(Δ)
-
如果 e(Vi,P′)=e(uipki+Ri,W)e(uiQi+Ri,P0′) 成立,则输出 1;否则输出 0
正确性证明:代入Vi=uisviψ(W)+uidi+ri(ψ(W)+P0),di=sQi,P0=sP,P0′=sP′,pki=sviP,Ri=riP,有
e(Vi,P′)=e(uisviψ(W)+uidi+ri(ψ(W)+P0),P′)
=e(uisviψ(W),P′)⋅e(uidi,P′)⋅e(riψ(W),P′)⋅e(riP0,P′)
=e(uisviP,W)⋅e(uisQi,P′)⋅e(riP,W)⋅e(riP,P0′)
=e(uipki,W)⋅e(uiQi,sP′)⋅e(Ri,W)⋅e(Ri,P0′)
=e(uipki+Ri,W)e(uiQi+Ri,P0′)
1.1.7 批量验证
BatchVerify({Mi,σi,UIDi,pki}i=1n):验证者批量验证消息 - 签名对 (Mi,σi)
-
随机选取 θ=(θ1,θ2,...,θn),其中 θi∈{0,1}l,l 为小整数
-
计算 Qi=H0(UIDi),ui=H1(UIDi∣∣Mi∣∣pki∣∣Ri∣∣Δ),W=H2(Δ)
-
如果 e(∑i=1nθiVi,P′) = e(∑i=1nθi(uipki+Ri),W)e(∑i=1nθi(uiQi+Ri),P0′) 成立,则输出 1;否则输出 0
正确性证明:代入Vi=uisviψ(W)+uidi+ri(ψ(W)+P0),di=sQi,P0=sP,P0′=sP′,pki=sviP,Ri=riP,有
e(∑i=1nθiVi,P′)=e(∑i=1nθi(uisviψ(W)+uidi+ri(ψ(W)+P0)),P′)
=e((∑i=1nθiuisvi)⋅ψ(W),P′)⋅e(∑i=1nθiuidi,P′) ⋅e((∑i=1nθiri)⋅ψ(W),P′)⋅e((∑i=1nθiri)⋅P0,P′)
=e((∑i=1nθiuisvi)⋅P,W)⋅e(∑i=1nθiuisQi,P′)⋅e((∑i=1nθiri)⋅P,W)⋅e((∑i=1nθiri)⋅P,P0′)
=e(∑i=1nθiuipki,W)⋅e((∑i=1nθiuiQi,sP′)⋅e(∑i=1nθiRi,W)⋅e(∑i=1nθiRi,P0′)
=e(∑i=1nθi(uipki+Ri),W)e(∑i=1nθi(uiQi+Ri),P0′)
1.2 车对车通信方案 ES&PPS
1.2.1 系统初始化阶段
在此阶段,KGC 生成系统主密钥并公布参数列表
-
给定安全参数 k,运行 Setup(k) 算法,生成主密钥 s 和参数列表 paramList={G1,G2,ψ,GT,e,q,P,P′,P0,P0′,H0,H1,H2}
-
选择一个安全的对称加密方案 Ekey(⋅)/Dkey(⋅) 及其密钥 key
-
设置系统主密钥为 (key,s)
-
公开参数列表 paramList′={paramList,Ekey(⋅)/Dkey(⋅)}
1.2.2 车辆注册阶段
车辆需要向 KGC 注册,KGC 会为每辆车生成部分私钥和假名,并通过安全信道发送给每辆车;车辆收到后,生成完整私钥及对应公钥
-
车辆 Vi 首先通过安全信道向 KGC 提交注册请求 (UIDi,m~),其中 UIDi 是车辆的真实身份,m~ 是请求的新假名数目
-
收到来自 Vi 的注册请求后,KGC 执行以下步骤:
- 计算 PIDi,j=Ekey(UIDi∣∣j)∣∣ti 生成一组假名,其中 ti 是假名有效期,j∈{1,…,m~}
- 运行 PPKE(PIDi,j,s) 算法,获得与 PIDi,j 对应的部分私钥 di,j
- 通过安全信道向 Vi 发送 {(PIDi,j,di,j)}j=1m~
-
车辆 Vi 分别运行 SPRK(PIDi,j,di,j) 和 SPK(PIDi,j,svi,j) 算法,生成相应的完整私钥 ski,j=(svi,j,di,j) 和公钥 pki,j
1.2.3 签名生成阶段
在车载自组网中,车辆需要定期广播交通相关信息 TRM。每辆车首先使用自己的完整私钥对 TRM 签名,再将签名后的 TRM 广播给附近车辆
-
运行 Sign(Mi,ski,j,PIDi,j,pki,j) 算法生成对 Mi 的签名 σi,j
-
Vi 广播 {PIDi,j,pki,j,Mi,σi,j} 为签名后的 TRM
1.2.4 验证阶段
车辆可能在短时间内收到许多 TRM,可批量验证一组 TRM 的有效性。假设 Vi 需要广播的 TRM 为 Mi,其中包含时间戳 Tsi,则
-
车辆运行 BatchVerify({Mi,σi,j,PIDi,j,pki,j}i=1n) 算法验证这些已签名 TRM 的有效性。如果输出 1,则接受这些 TRM
1.2.5 追踪阶段
如果车辆发现了使用伪造签名的 TRM,可以请求 KGC 披露签名者的真实身份
-
KGC 计算 Dkey(PIDi,j)=Dkey(Ekey(UIDi∣∣j)) 得到 UIDi∣∣j,从而获知其真实身份 UIDi
2 安全性分析
2.1 安全规约回顾
安全规约中涉及的三类实体:
-
敌手(Adversary):意图攻破密码学方案的实体;
-
挑战者(Challenger):当敌手与真实方案(Real Scheme)交互时,敌手实际上是在与挑战者交互,由挑战者生成真实方案并应答敌手的询问请求。挑战者仅出现在安全模型和安全描述中;
-
模拟器(Simulator):当敌手与模拟方案(Simulated Scheme)进行交互时,敌手实际上是在与模拟器进行交互,由模拟器生成模拟方案并应答来自敌手的询问请求。模拟器仅出现在安全归约中,作为运行归约算法的一方。
2.2 无证书签名的安全模型
2.3 本文 CLSS 的模拟方案
底层困难问题 co-CDHP:已知 {P,aP,P′,bP′∣a,b∈Zq∗},求解 abP 是困难的。模拟方案包含以下步骤:
-
Setup
-
PPK(UIDi) query
-
SVE(UIDi) query
-
PK(UIDi) query
-
PKR(UIDi,pki′) query
-
S(Mi,UIDi,pki′) query
-
Forgery
注:本文在规约时全程使用了 Challenger 同敌手进行交互,这是不严谨的。由于挑战者只会如实地回答敌手的询问,这就导致无法将方案规约到困难问题上
2.4 求解困难问题
e(Vi∗,P′)=e(ui∗pki∗+Ri∗,Wi∗)e(ui∗Qi∗+Ri∗,P0′) ①
e(Vi∗′,P)=e(ui∗′pki∗+Ri∗,Wi∗)e(ui∗′Qi∗+Ri∗,P0′) ②
Type I:由P0′=aP′,Qi∗=αi∗bP,①-②得
abP=αi∗−1[(ui∗−ui∗′)−1(Vi∗−Vi∗′)−γi∗pki∗] 为困难问题的解
Type II:由Wi∗=βi∗aP′,pk∗=svi∗bP,①-②得
abP=svi∗−1βi∗−1[(ui∗−ui∗′)−1(Vi∗−Vi∗′)−sQi∗] 为困难问题的解
2.5 非形式化安全性证明
消息认证:车辆 Vi 在广播包含时间戳 Tsi 的交通相关消息(TRM)Mi 前,首先运行 Sign(Mi,ski,j,PIDi,j,pki,j) 算法生成 {PIDi,j,pki,j,Mi,σi,j} 为签名后的 TRM。当车辆 Vj 接收到 n 个消息 - 签名对时,使用算法 BatchVerify({Mi,σi,j,PIDi,j,pki,j}i=1n) 验证其有效性。根据定理 1 和 2,已签名的 TRM 是不可伪造的。
条件隐私:车辆 Vi 使用假名 PIDi,j 保护其真实身份,假名基于安全对称加密方案 Ekey(⋅)/Dkey(⋅) 生成,在不知道对称密钥的情况下,任何实体都无法恢复 Vi 的真实身份 UIDi。仅 KGC 拥有密钥,具备恢复 Vi 的真实身份 UIDi 的能力。
3 实验评估
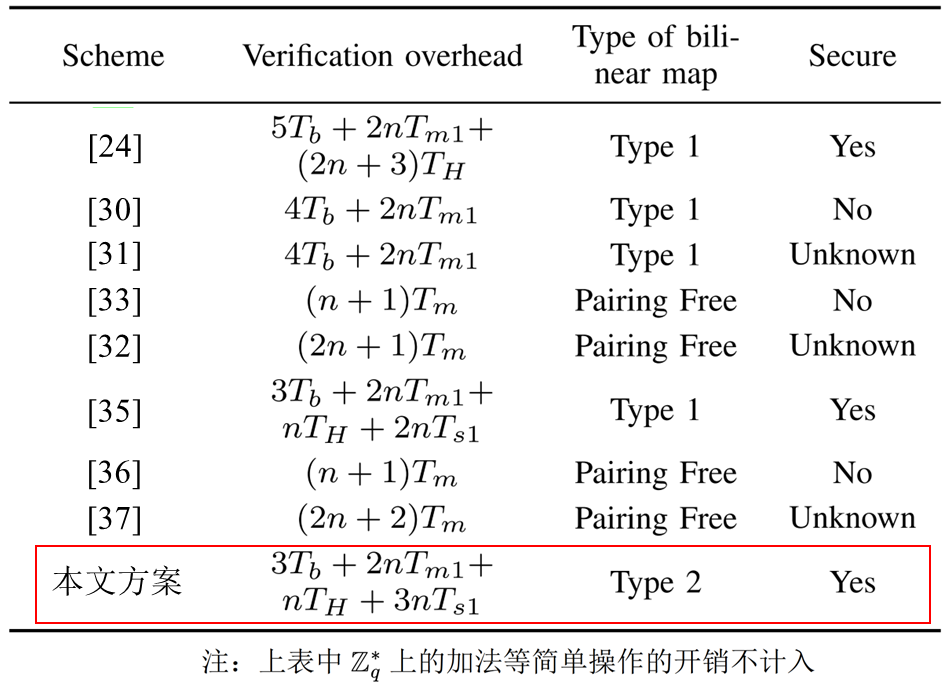
3.1 计算开销
![]()
-
Tb:执行双线性映射操作的时间
-
Tm1:执行 G1 上标量乘法操作的时间
-
Tm:执行椭圆曲线上标量乘法操作的时间
-
TH:执行映射到点的哈希时间
-
Ts1:执行 G1 上小指数测试的时间
本文此处援引了 Yang et al. 一文,意在说明:I 型双线性映射操作要比 II 型更为昂贵,使用 I 型双线性映射的 Tb、Tm1、TH 和 Ts1 值显著高于使用 II 型双线性映射设计的方案(译)
![]()
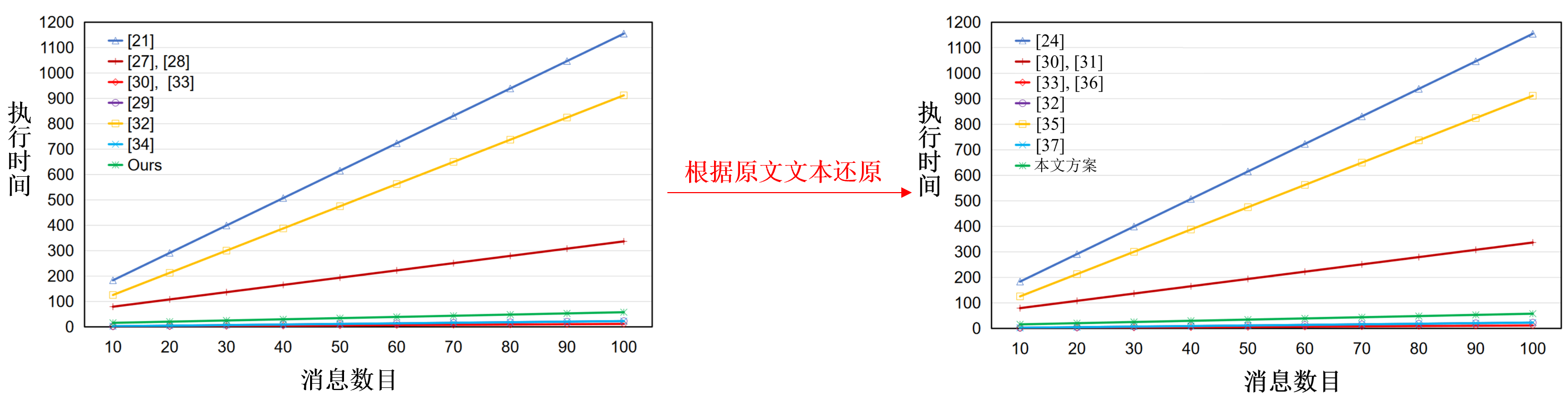
按照逻辑,为呼应本文 “方案计算开销低于其他支持批量验证、安全的无证书签名方案” 的主要贡献,此处应当着重比较文献 [35] 等,但原文图例标注有误导致无法一一对应。ES&PPS 的批量验证效率仍低于无配对的四种方案([32],[33],[36],[37]),但这些方案是不安全的,或缺少安全性证明。
3.2 通信开销
![]()
-
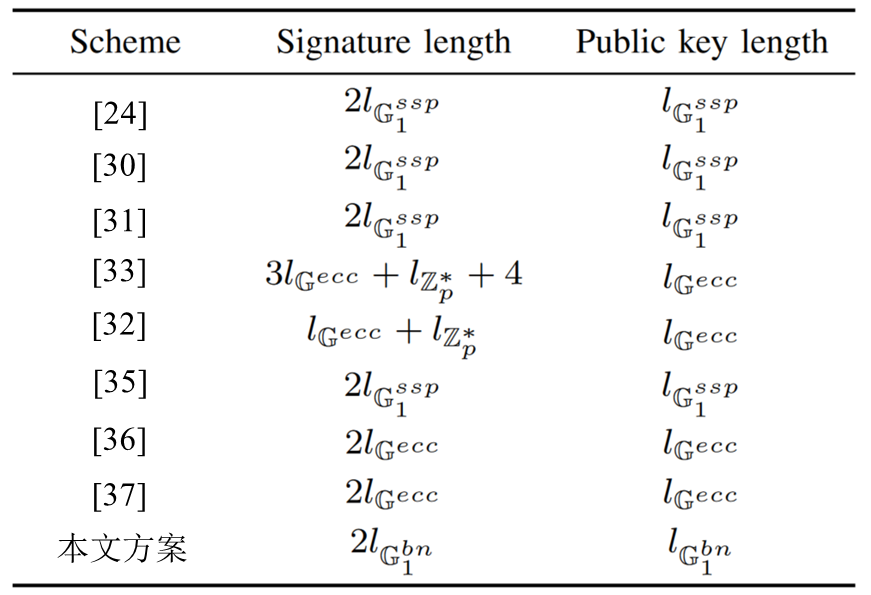
lZp∗:32 字节,Zp∗ 中的元素长度
-
lG1ssp:192 字节,SSP 曲线上 G1 中的元素长度
-
lG1bn:32 字节,BN 曲线上 G1 中的元素长度
-
lGecc:32 字节,BN 曲线上任意群的元素长度
对 II 型双线性配对,已知采用的曲线为 BN256,则为达到 128bit 安全长度,需要 ∣g1∣≥256(bits),故群元素的大小为 256÷8=32 字节。对比表明,本文方案在签名和公钥长度方面具有相同或更低的传输开销。